From Mixtures to Hierarchical Mixtures (a.k.a. Probabilistic Circuits)¶
A probabilistic perspective on modeling, generalization, learning and inference¶
Random variables and probability distributions Let us imagine cats. Most people like cats, some people are crazy in love with cats. There are ginger cats, black cats, big cats, small cats, puffy cats, furless cats. In fact, there are many different kinds of cats. However, when I say this word: "a cat", everyone has some kind of a cat in their mind. One can close eyes and "generate" a picture of a cat, either their own cat or a cat of a neighbor. Further, this "generated" cat is located somewhere, e.g., sleeping on a coach or in a garden chasing a fly, during a night or during a day, and so on. Probably we can agree at this point that there are infinitely many possible scenarios of cats in some environments.
Why to think of cats? In fact, we can think of any other object in the world. Formally, we can define a space of all objects in the world as $\omega \in \Omega$. For simplicity, we consider only physical objects that an AI system (either embodied or not) could perceive through its sensors. Without a loss of generality, I would claim that even an AI-powered app deals with physical objects through, e.g., a camera, or images taken by a user through a camera. The AI system processes the input signals through some functions that return, e.g., continuous values like analog signals, discrete values like text from a conversation, or bits like digital signals. These functions are called random variables. For instance, a robot with a camera can take an RGB photo (e.g., of a cat) of the height $H$ and the width $W$ that defines a random variable. Typically, a random variable is denoted by $\mathbf{x} (\omega)$ or $\mathbf{x}$ for short. In our example, for images taken by a digital camera, we get $\mathbf{x}: \Omega \rightarrow \{0,\ldots , 255\}^{3 \times H \times W}$. In general, $\mathbf{x}: \Omega \rightarrow \mathcal{E}$ where $\mathcal{E}$ is a $D$-dimensional measurable space (in the sense of measure theory), e.g., $\mathcal{E} = \mathbb{R}^D$, $\mathcal{E} = \{0,1\}^D$.
Random variables are called random because their outcomes are not necessarily predictable due to unobserved factors.
A side note: If we think about randomness, this simple introduction could very quickly turn into a very deep philosophical discourse. If you disagree with me, my curious reader, it is ok! But I hope that we can agree with these statements provided above and move on.
In other words, if one takes theirs cat and takes a series of photos, the resulting pixels could take various values due to lighting, breathing of their cat, shaking hand, etc.; in general, some factors that are neither controlled nor explicitely measured. This series of photos, taken at different times of a day, or even on different days, we call observations, $\mathcal{D} = \{\mathbf{x}_{1}, \mathbf{x}_{2}, \ldots , \mathbf{x}_{N}\}$. There is some randomness in the process of taking photos, but still some pixel values are highly improbable or even impossible. For instance, a cat has four legs, a single head or its fur cannot be naturally pink, and so on. As a result, we can say that there exists a distribution of pixel values (values of random variables) that correspond to less likely values or more likely values. Formally, we say that there exists some probability distribution of a random variable $\mathbf{x}$, denoted as $p(\mathbf{x})$, such that: $\forall_{\mathbf{x}} p(\mathbf{x}) \in [0,1]$ and (discrete case) $\sum_{\mathbf{x}} p(\mathbf{x}) = 1$, (continuous case) $\int_{\mathbf{x}} p(\mathbf{x}) \mathrm{d} \mathbf{x} = 1$. There are multiple nice properties of probability distributions, and two of them are especially useful in modeling and inference (for simplicty, for two random variables $\mathbf{x} = (x_1, x_2)$):
- the sum rule: $p(x_1) = \sum_{x_2} p(x_1, x_2)$,
- the product rule $p(x_1, x_2) = p(x_1 | x_2) p(x_2)$ or $p(x_1, x_2) = p(x_2 | x_1) p(x_1)$.
The sum rule shows us how to "get rid of" some random variable in a probabilistic manner. The product rule indicates how to express a joint distribution using conditional distributions.
In the product rule, we see a conditional distribution, i.e., a distribution over one random variable given information about the other random variable. The conditional distribution is a distribution, namely, it sums to $1$ and returns values between $0$ and $1$. If two random variables are independent (stochastically), e.g., $x_1$ is independent of $x_2$, then $p(x_1 | x_2) = p(x_1)$. In plain words, no matter what information we provide about $x_2$, there is no change in the distribution of $x_1$. As a result, the product rule results in $p(x_1, x_2) = p(x_1) p(x_2)$.
Modeling In general, this is useful to think of some true probability distribution for a given random variable. However, this could be also misleading. Again, we can turn this dry sentence into a long discussion. Therefore, from time to time, we will refer to some abstract true distribution if needed, but practically, we will use some empirical distribution defined by observations $\mathcal{D}$ instead. Formally, we define the empirical distribution as a sum of peaks:
where $\delta(\mathbf{x} - \mathbf{x}_n)$ for $\mathbf{x} \neq \mathbf{x}_n$ equals 0 and for $\mathbf{x} = \mathbf{x}_n$ equals $+\infty$ in the continuous case (Dirac's delta), and $1$ in the discrete case (Kronecker's delta).
Please remember, my curious reader, that this is mathematics, we need that to communicate easily and to express our thoughts crisply. It is not magic, even though, sometimes, it sounds complicated. If you are not familiar with these terms, no worries. You will get used to those and, as you will see, they are quite useful.
Very often we assume that observations come from the same true distributions and all observations were achieved independently. This is referred to as identically and independently distributed (iid) data. These two statements mean that: (i) all $\mathbf{x}_n \in \mathcal{D}$ follow the same distribution, and (ii) all $\mathbf{x}_n$'s are independent from each other, i.e., $p(\mathbf{x}_1, \mathbf{x}_2, \ldots, \mathbf{x}_N) = \prod_{n=1}^{N} p(\mathbf{x}_n)$.
Alright, but why do introduce all these concepts? When it becomes interesting? These are the questions that pinch your brain, my curious readers, aren't they? They are fascinating if we could formulate a model distribution (or simply a model) of the world (or the tiny piece of the world we consider), namely, $p(\mathbf{x} ; \theta)$. As you can notice, we introduced a new quntity $\theta$ that denote some parameters of the model. But what is this model, what is its form? It depends on the character of observed data. For instance, for real-valued data, an appropriate distribution can be a Gaussian (normal) distribution:
\begin{align} p(\mathbf{x} ; \theta) &= \frac{1}{\sqrt{(2 \pi)^{D} |\Sigma|}} \exp\left( -\frac{1}{2} (\mathbf{x} - \mu)^{\top} \Sigma^{-1} (\mathbf{x} - \mu) \right) ,\\ &\stackrel{df}{=} \mathcal{N}(x | \mu, \Sigma), \end{align}
where $\theta = (\mu, \Sigma)$, $\mu$ denote location parameters (a.k.a. means) and $\Sigma$ denotes scale parameters (a.k.a. the covariance matrix with variances on the diagonal).
However, if our data is discrete, we use a Bernoulli distribution for binary data (i.e., $x_d \in \{0, 1\}$:
\begin{align} p(\mathbf{x} ; \theta) &= \prod_{d=1}^{D} \theta_d^{x_d} (1 - \theta_d)^{1-x_d} ,\\ &\stackrel{df}{=} \mathrm{Bern}(x ; \theta), \end{align}
or a Categorical distribution for categorical data (i.e., discrete and unordered, $x_d \in \{0, 1, \ldots, K-1\}$):
\begin{align} p(\mathbf{x} ; \theta) &= \prod_{d=1}^{D} \prod_{k=1}^{K} \theta_{dk}^{\mathbb{1}[x_d = k]} ,\\ &\stackrel{df}{=} \mathrm{Cat}(x ; \theta), \end{align}
where $\mathbb{1}[x = k]$ is the indicator function that returns $1$ if $x$ equals $k$ and $0$ - otherwise. Interestingly, $\theta$'s in a Bernoulli distribution and a Categorical distribution have very specific meanings, respectively, $\theta_{d} = p(x_d = 1 ; \theta)$ and $\theta_{dk} = p(x_d = k ; \theta)$.
Learning Once we pick a distribution for our model, we can now ask the fundamental question: How to obtain the values of parameters $\theta$, i.e., how to estimate $\theta$? This is what AI people call learning or training. In the probabilistic setting, it is typically done by fitting our model to the empirical distribution by minimizing some distance metric. For instance, it can be accomplished by minimizing the Kullback-Leibler divergence with respect to the parameters $\theta$:
\begin{align} KL\left[ p_{data}(\mathbf{x}) || p(\mathbf{x} ; \theta) \right] &= \sum_{\mathbf{x}} p_{data}(\mathbf{x}) \log \frac{ p_{data}(\mathbf{x}) }{ p(\mathbf{x} ; \theta) } \\ &= \sum_{\mathbf{x}} p_{data}(\mathbf{x}) \log p_{data}(\mathbf{x}) - \sum_{\mathbf{x}} p_{data}(\mathbf{x}) \log p(\mathbf{x} ; \theta) \\ &= C - \sum_{\mathbf{x}} p_{data}(\mathbf{x}) \log p(\mathbf{x} ; \theta) \\ &= C - \sum_{\mathbf{x}} \sum_{n=1}^{n} \delta(\mathbf{x} - \mathbf{x}_{n}) \log p(\mathbf{x} ; \theta)\\ &= C - \sum_{n=1}^{n} \log p(\mathbf{x}_n ; \theta) \end{align}
where $C$ is the negative entropy of the empirical distribution, which is independent of the paramters $\theta$, thus, irrelevant for learning the model, and the last step comes from a property of the delta function.
A side note: Please remember, my curious reader, that the Kullback-Leibler divergence is asymmetric, thus, where we place the empirical distribution and the model matters!
For the iid data, the term $\sum_{n=1}^{n} \log p(\mathbf{x}_n ; \theta)$ corresponds to the log-likelihood function, namely:
\begin{align} \log p(\mathcal{D} ; \theta) &\stackrel{df}{=} \log p(\mathbf{x}_1, \mathbf{x}_2, \ldots, \mathbf{x}_N ; \theta) \\ &\stackrel{iid}{=} \log \prod_{n=1}^{N} p(\mathbf{x}_n ; \theta) \\ &= \sum_{n=1}^{N} \log p(\mathbf{x}_n ; \theta) . \end{align}
In the second step, we use the fact that the observations come from the same distribution and all observations are independent from each other. The likelihood function plays a special role in the probabilistic modeling and serves as a starting point for many deep generative models.
Generalization As a quote from a famous British statistician named George Box indicates, all models are wrong but some are useful. They are wrong, fine. But what it means that some are useful?! Let us consider the following example in Figure 1. We have some observed data from a true distribution (here we use the so-called two moon problem) like in Figure 1.A. After fitting a model to those data, we end up with a density estimator in Figure 1.B. As you can notice, the model distribution assigns probability mass mainly where the data lies, however, it also assigns some probability mass in regions where little to no data is observed. Is it a good feature? My answer is yes, because this is what we expect from a model, to generalize to regions where no or little data was observed.
A

B
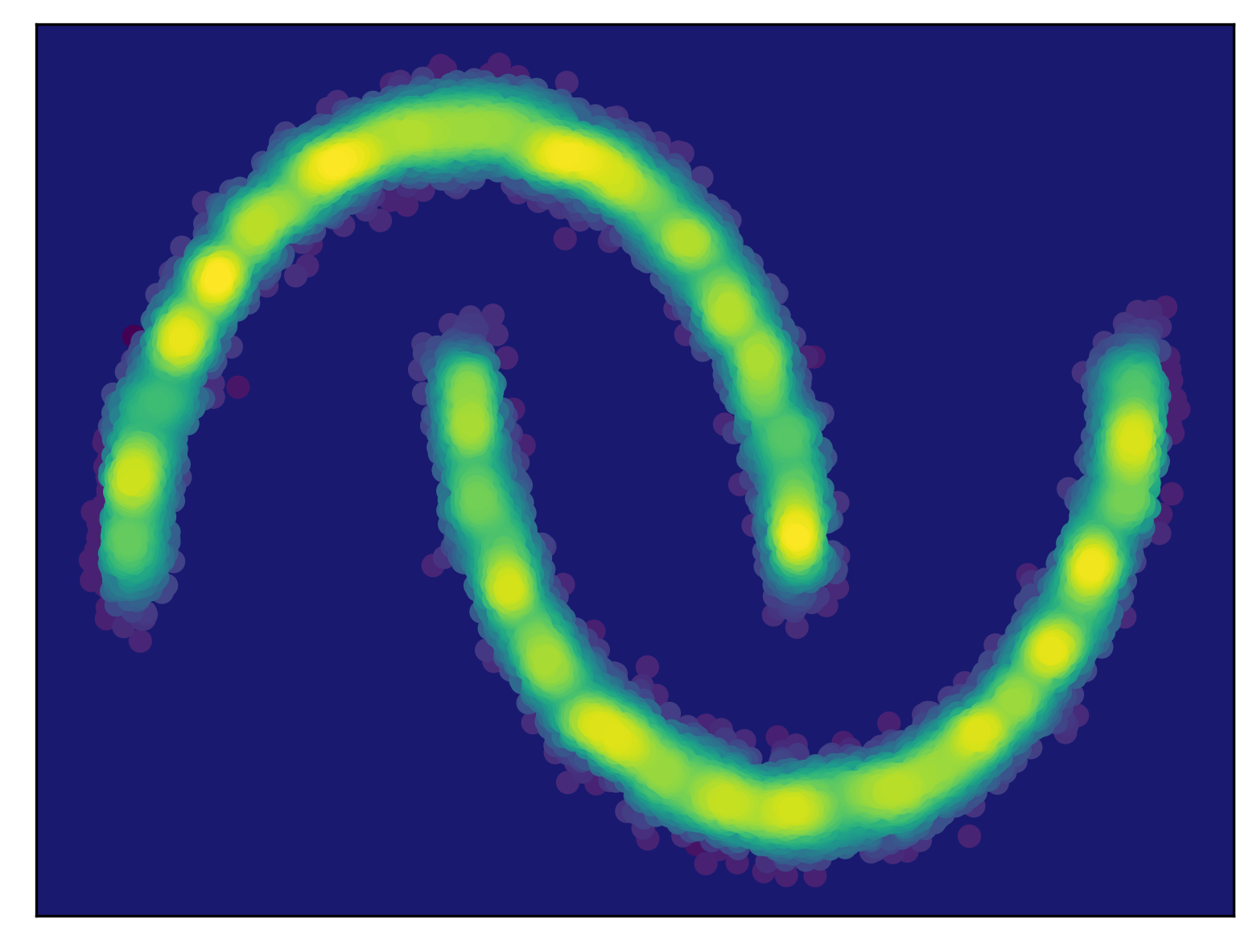
In machine learning, generalization is understood as model's ability to adapt properly to new, previously unseen data, drawn from the same distribution as the one used to create the model (Bishop, 2006). Here, adapting means to sample or to assign probability/likelihood. Hence, to be able to generalize, having a probabilistic model (i.e., a model distribution) is a key! Now we can see that some models are more useful than others because they can generalize better. Please keep it in mind while thinking of various deep generative models.
Inference After fitting a model to data, we can (finally!) use our model! The simplest uses of probabilistic models (either conditional or joint) are obtaining new data and calculating the likelihood function (also referred to as evidence), $p(\mathbf{x})$. I call these simple, however, these are quite powerful, if you think about it, my curious reader. But wait a second, are conditional models useful for generating new data? For instance, if $x_2$ is a weight of a cat and $x_1$ is a height of a cat, then one can say that sampling from $p(x_2 | x_1)$ is... generating new data, namely, pairs $(x_1, x_2)$. There is a thin and blurry line between discriminative (predictive) models and generative models, especially from a probabilistic perspective. After all, we deal with probability distributions and calling some models "discriminative" and others "generative" is not necessarily constructive. But, again, we will not delve into that discussion here, but instead we will focus on inference.
In the probabilistic modeling world, inference is the key to draw conclusions about stochastic dependencies and quantities. We can define inference as answering probabilities queries. Following (Choi et al., 2020), we can distinguish the following classes of probabilistic queries:
- (EVI) Calculating evidence $p(\mathbf{x})$.
- (MAR) Calculating marginals $p(\mathbf{x}_{-d}) = \int p(\mathbf{x})\ \mathrm{d} x_d$.
- (MAP) Calculating the most probable value, $\arg \max_{\mathbf{x}} p(\mathbf{x})$.
- Calculating advanced queries, e.g., about logical events.
Interestingly, not all classes of contemporary deep generative models can do EVI, and only a few provide MAR and/or MAP. Later, we will briefly discuss a class of models called Probabilistic Circuits (Choi et al., 2020) that can do EVI, MAR and MAP. But the rest of the deep generative models can calculate EVI at best.
Interlude: Probabilistic graphical models¶
As you can imagine, my curious reader, working with probabilistic models can be sometimes quite difficult, especially if the number of variables $D$ is large and there is a specific structure among random variables, i.e., complicated stochastic dependencies. For this purpose, to represent probability distributions, probabilistic graphical models (PGMs) were proposed (Koller & Friedman, 2009). In a nutshell, a PGM is a probabilistic model for which a graph expresses the conditional dependence structure between random variables. There are undirected graphical models in which nodes are random variables and edges imply some sort of dependence among them, a.k.a. Markov networks. A more straightforward class of PGMs is a class of Bayesian networks that are directed acyclic graphs with directed edges denoting conditional dependencies and random variables being nodes.
Here, we will not go into details of various PGMs, interested (and curious!) readers can check (Koller & Friedman, 2009) as a fantastic primer. It is good to know though that for generative modeling, Bayesian networks are useful in thinking in a generative manner. Why? Because they are acyclic meaning that there are no cycles, i.e., a path starting and ending in the same random variable. Clearly, a cycle disallows a proper generative process (if a random variable $x_{A}$ depends on $x_{B}$ and the other way around, how we can generate $x_{A}$ and $x_{B}$?).
A side note: Not all probability distributions could be represented as Bayesian networks. Please be aware of that! Therefore, ther are some generative models that go beyond Bayesian networks. However, to get familiar with generative processes, Bayesian networks give a good starting point for that.
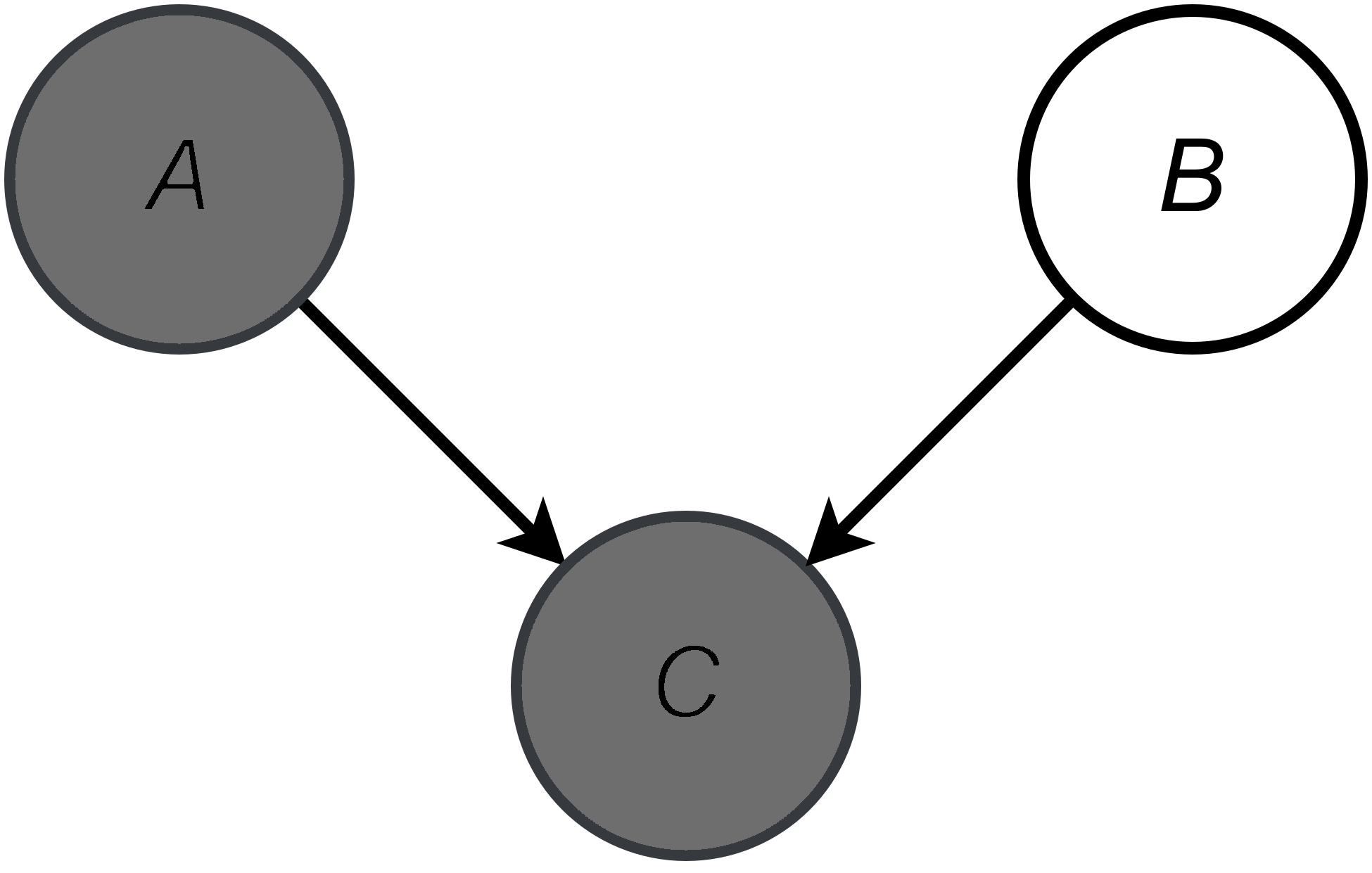
An example of a Bayesian network is presented in Figure 2. A gray node denotes an observable variable, a white node is a latent variable and arrows determine conditional dependencies. The corresponding joint distribution in the example in Figure 2 is the following:
\begin{equation} p(A, B, C) = p(C | A, B)\ p(A)\ p(B) . \end{equation}
If we would like to calculate the marginal distribution over observable variables, we need to sum out the latent variable, namely:
\begin{align} p(A, C) &= \sum_{B} p(A, B, C) \\ &= \sum_{B} p(C | A, B)\ p(A)\ p(B). \end{align}
Mixture models¶
Modeling with Mixture of Gaussians (MoG) Take a deep breath. A lot of information so far, I am aware of that, my curious reader. Take a short break if needed, make a coffee. And backle up, we are going to get all the information together and propose one of the simplest yet very effective generative model: a mixture model. Here we go!
Let us consider the following situation. We have a random variable $x$ denoting a weight of cats. There are female cats and male cats, and they differ in weights. We model the true distribution for female cats using a Gaussian, and another Gaussian for modeling the true distribution for male cats. Then someone asks us what is the overall distribution over weights of cats (no distrinction between female and male cats). We are given some iid data of weights of cats but with no information about the gender of observed cats, just pure numbers of their weights. How can we approach this problem?
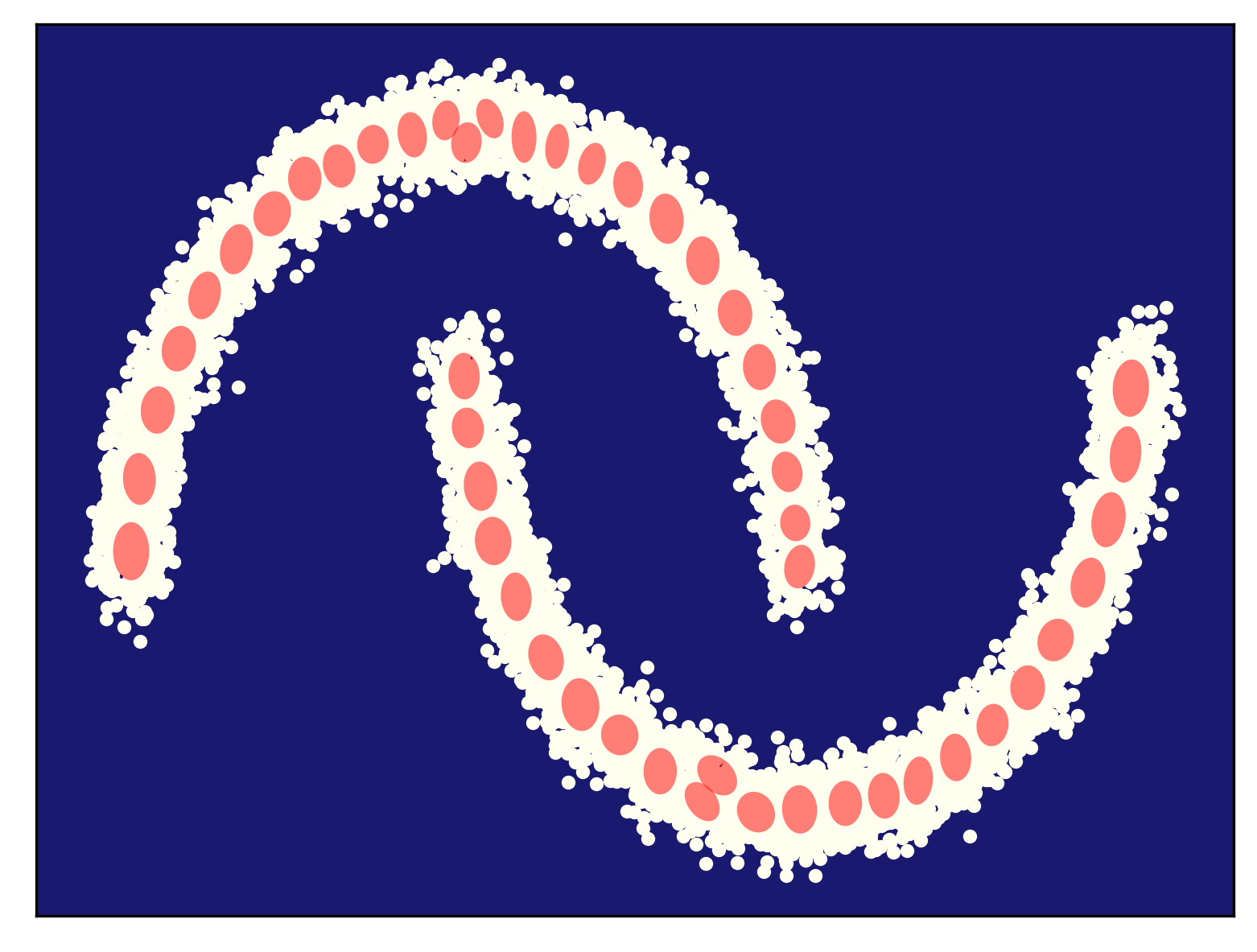
We can start with random variables. OK, $x$ denotes weight and it is an observable random variable. With a small abuse of reality, we assume that $x \in \mathbb{R}$. Next, we know that there is the biological sex of cats $z \in \{0, 1\}$, where $z = 0$ for female cats and $z = 1$ for male cats. However, $z$ is an unobserved (latent) variable. Further, we know that the sex, $z$, influences the weight, $x$. The resulting probrabilistic graphical model is presented in Figure 3.
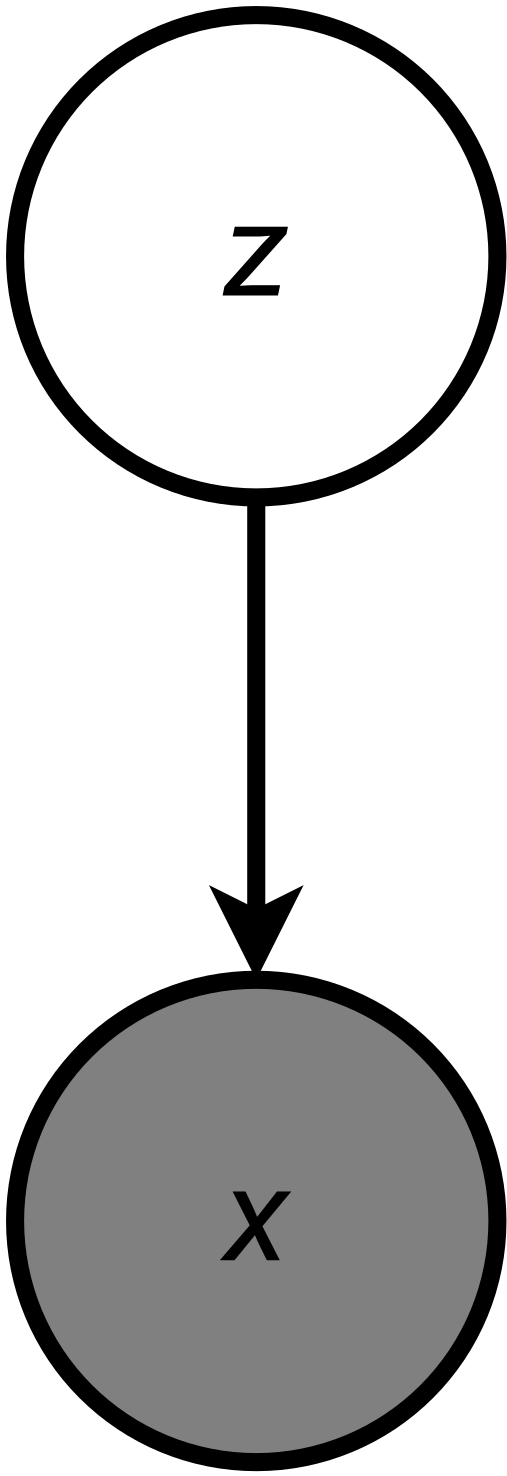
Let us write the joint distribution and use the product rule according to the PGM in Figure 3:
\begin{equation} p(x,z) = p(x | z)\ p(z) . \end{equation}
So far, so good! Since $x$ is real-valued and $z$ is binary, we can use a Gaussian distribution and a Bernoulli distribution, respectively, to model them:
\begin{equation} p(x,z) = \mathcal{N}(x | \mu(z), \sigma^{2}(z))\ \mathrm{Bern}(z | \omega) , \end{equation}
where we indicate the dependence between $x$ and $z$ through the mean and the variance, i.e., the parameters of the Gaussian are different for different values of $z$.
Now, please remember, my curious reader, that we have some observations $\mathcal{D} = \{x_1, x_2, \ldots, x_N\}$. Since we do not observe $z$, we should marginalize it out using the sum rule, namely:
\begin{align} p(x) &= \sum_{z} p(x,z) \\ &= \sum_{z} \mathcal{N}(x | \mu(z), \sigma^{2}(z))\ \mathrm{Bern}(z | \omega) \\ &= \mathcal{N}(x | \mu(z=0), \sigma^{2}(z=0))\ \mathrm{Bern}(z=0 | \omega) + \mathcal{N}(x | \mu(z=1), \sigma^{2}(z=1))\ \mathrm{Bern}(z=1 | \omega) \\ &= (1 - \omega)\ \mathcal{N}(x | \mu_0, \sigma_0^{2}) + \omega\ \mathcal{N}(x | \mu_1, \sigma_1^{2}) , \end{align}
where we used $\mu_i \equiv \mu(z=i)$ and $\sigma_{i}^{2} \equiv \sigma^{2}(z=i)$ to keep the notation uncluttered.
Let us get back to our cats and their weights (a disclaimer: all values are made up and they serve educational purposes!). An example of a mixture of two Gaussians is presented in Figure 4. In Figure 4.A, the two mixture components are visualized separately while in Figure 4.B the marginal distribution, $p(x)$, is presented. Note that the two components have different component probabilities $\omega_0$ and $\omega_1=1 - \omega_0$. Moreover, in Figure 4.B, the region where the two components overlap is summed.
A
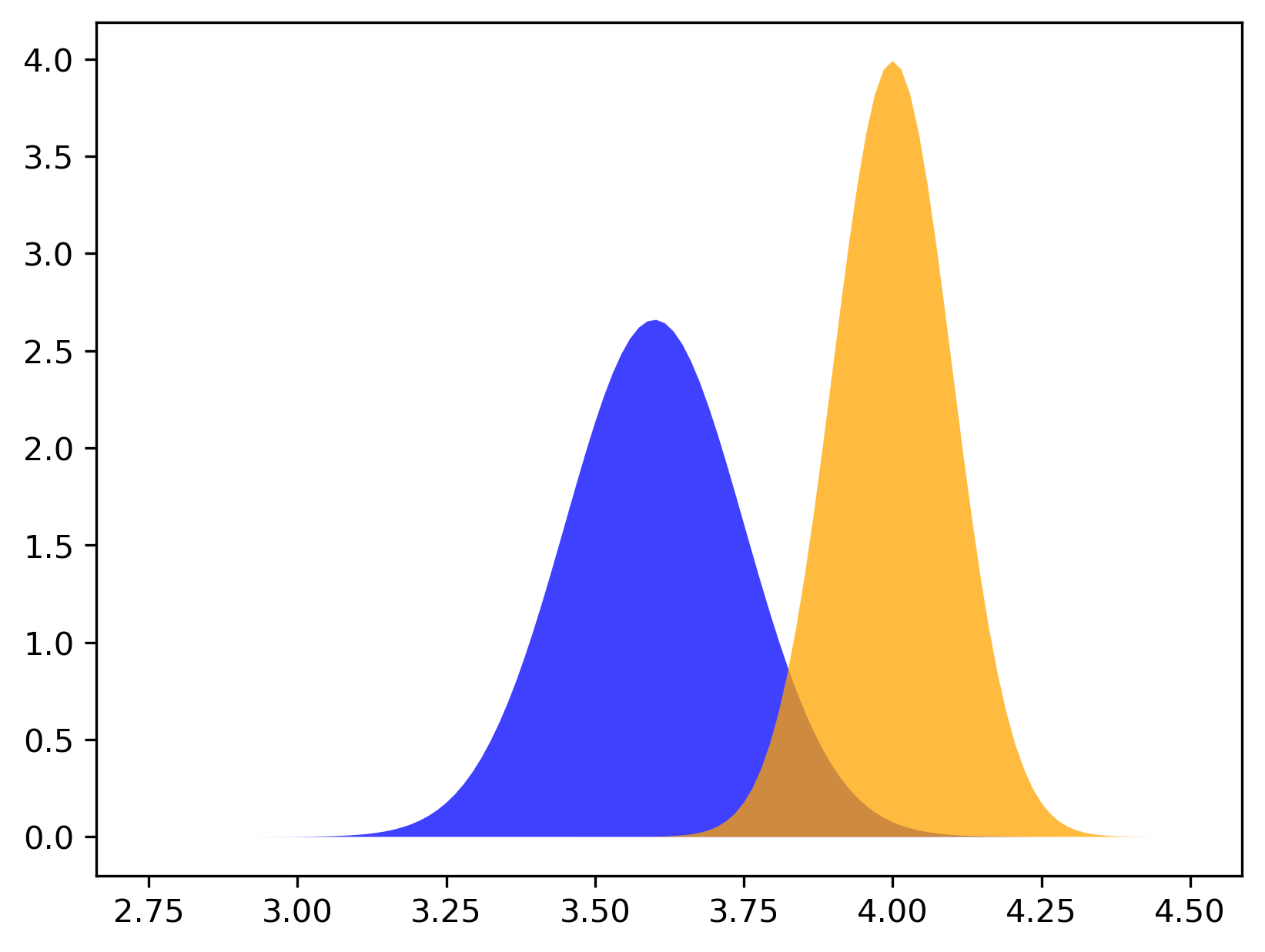
B
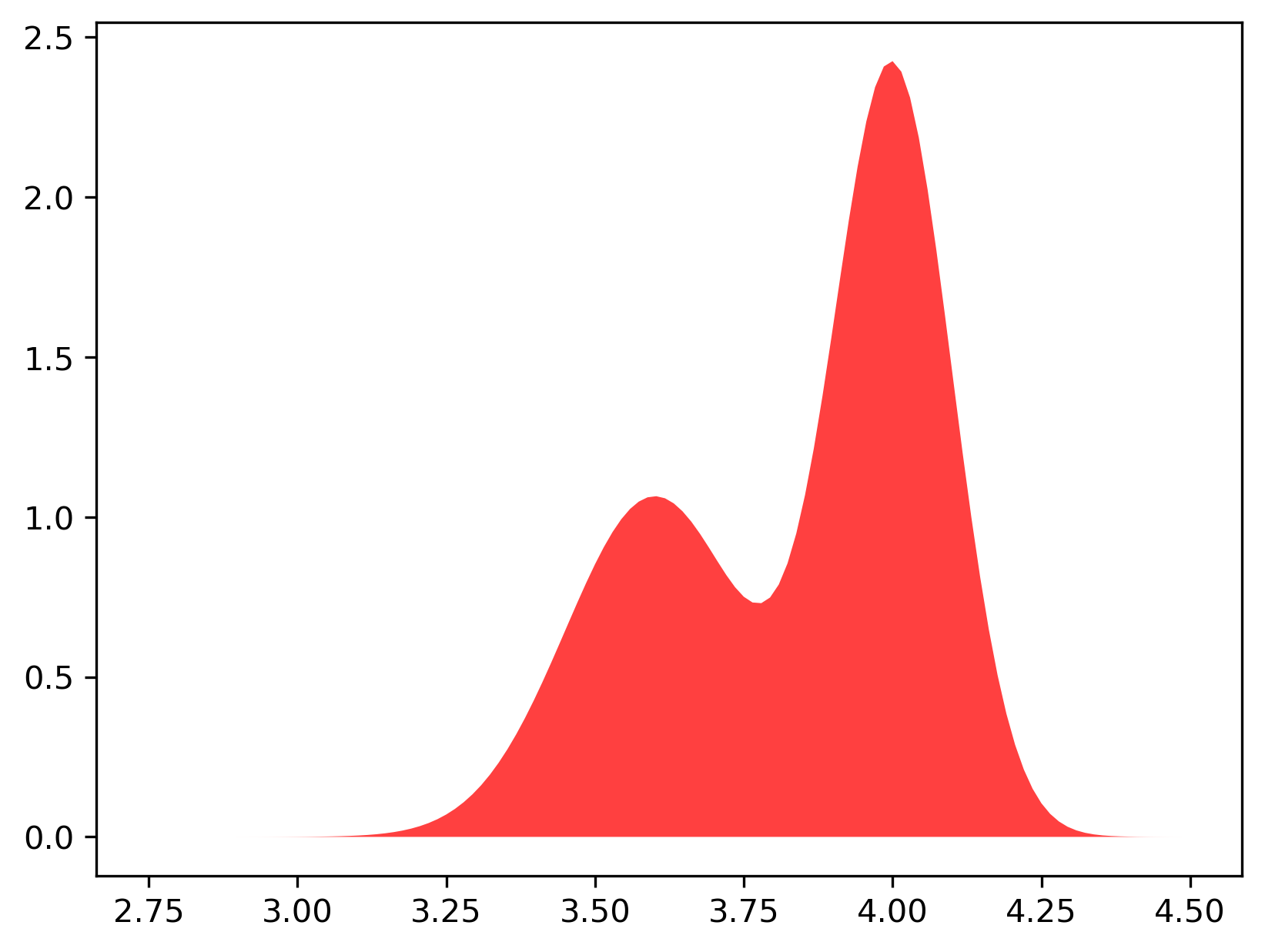
In general, we define a mixture of Gaussians (MoG) with $K$ components as follows:
\begin{align} p(x; \theta) &= \sum_{z} \mathcal{N}(x | \mu(z), \sigma^{2}(z))\ \mathrm{Cat}(z | \omega) \\ &= \sum_{k=0}^{K=1} \omega_k\ \mathcal{N}(x | \mu_k, \sigma^{2}_k) . \end{align}
Training: The log-likelihood function Alright, let us continue our example with two components and think of how we can train a mixture of Gaussians. First, we need to set up the stage, namely, calculate the log-likelihood function. For given data $\mathcal{D}$, the likelihood function is the following:
\begin{align} p(\mathcal{D} ; \mu_0, \mu_1, \sigma_0^2, \sigma_1^2, \omega) &= \prod_{n=1}^{N} p(x_n ; \mu, \sigma^2, \omega) \\ &= \prod_{n=1}^{N} \left( (1 - \omega)\ \mathcal{N}(x_n | \mu_0, \sigma_0^{2}) + \omega\ \mathcal{N}(x_n | \mu_1, \sigma_1^{2}) \right) \end{align}
and the log-likelihood function is the following (we take the logarithm to work with sums instead of products; the logarithm does not change the position of the optimum):
\begin{equation} \log p(\mathcal{D} ; \mu_0, \mu_1, \sigma_0^2, \sigma_1^2, \omega) = \sum_{n=1}^{N} \log \left( (1 - \omega)\ \mathcal{N}(x_n | \mu_0, \sigma_0^{2}) + \omega\ \mathcal{N}(x_n | \mu_1, \sigma_1^{2}) \right) . \end{equation}A few comments here:
- The parameters of our model are $\theta = (\mu_0, \mu_1, \sigma_0^2, \sigma_1^2, \omega)$.
- The (log-)likelihood function has a nice interpretation: How likely are the observed data for given values of parameters $\theta$?
- The log-likelihood function can be taken as the objective/training function and optimized with respect to the parameters $\theta$ to find the most likely parameters that generated the observed data.
Further, we (yes, you and me, my curious reader!) notice that it would be easier to deal with $\log \mathcal{N}(x | \mu, \sigma^2)$ instead of $\mathcal{N}(x | \mu, \sigma^2)$ because of the cumbersome $\exp$ in Gaussians. Taking the log gives:
\begin{align} \log \mathcal{N}(x | \mu, \sigma^2) &= \log \left( \frac{1}{\sigma \sqrt{2\pi}} \exp\left\{ -\frac{1}{2} \left( \frac{x - \mu}{\sigma}\right)^2 \right\} \right) \\ &= - \frac{1}{2}\log 2\pi - \frac{1}{2} \log \sigma^2 - \frac{1}{2\sigma^2} (x - \mu)^2 . \end{align}
Now, if only we could get the logarithm inside the sum, it would be easier! But we can't... However, do we need to do that? We can use the property of exp and log: $\exp(\log(x)) = x$. Let us use that to the log-likelihood function:
\begin{align}
\log p(\mathcal{D} ; \mu_0, \mu_1, \sigma_0^2, \sigma_1^2, \omega) &= \sum_{n=1}^{N} \log \left( \exp\left(\log\left((1 - \omega)\ \mathcal{N}(x_n | \mu_0, \sigma_0^{2})\right)\right) + \exp\left(\log\left(\omega\ \mathcal{N}(x_n | \mu_1, \sigma_1^{2}) \right)\right) \right) \\
&= \sum_{n=1}^{N} \log \left( \exp\left(\log\left(1-\omega\right) + \log \mathcal{N}(x_n | \mu_0, \sigma_0^{2}) \right) + \exp\left(\log\left(\omega\right) + \log \mathcal{N}(x_n | \mu_1, \sigma_1^{2}) \right) \right) \\
&= \sum_{n=1}^{N} \log \left( \sum_{i=0}^{1} \exp\left(\log\left(\omega_i\right) + \log \mathcal{N}(x_n | \mu_i, \sigma_i^{2}) \right) \right) \\
&= \sum_{n=1}^{N} \log \left( \sum_{i=0}^{1} \exp\left( a_i \right) \right) .
\end{align}
A few comments:
- As you noticed, my curious reader, we introduced $a_i \stackrel{df}{=} \log\left(\omega_i\right) + \log \mathcal{N}(x_n | \mu_i, \sigma_i^{2})$. It will be very creal why in a second.
- We quite artificially introduced another sum so that you can get familiar with notation but also to see that we can deal with more than two components in the same manner.
- In ML, the function $\log \left( \sum_{i=1}^{I-1} \exp\left( a_i \right) \right)$ has a specific name and it is called... the log-sum-exp (or LogSumExp, LSE) function. This function, in general, could result in underflow/overflow (i.e., it can be numerically unstable). To avoid that, we can use the following trick:
$$ LSE(a_0, \ldots, a_{I-1}) = a^* + LSE(a_0 - a^*, \ldots, a_{I-1} - a^*) , $$
where $a^* = \max \{a_0, \ldots , a_{I-1}\}$. Please remember this function because it plays a crucial role in many topics in AI. And if you do not want to make a mistake, always check first if a library you use provides the LSE function. Most of them do!
In general, the log-likelihood function for a MoG with $K$ components is defined as follows:
\begin{align} \log p(\mathcal{D} ; \theta) = \sum_{n=1}^{N} \log \left( \sum_{k=0}^{K-1} \exp\left( \log \omega_k + \log \mathcal{N}(x | \mu_k, \Sigma_k \right) \right) . \end{align}
Training: The algorithms Now we are ready to implement a training algorithm. Since we know the form of the log-likelihood function, we can pick any optimization algorithm we want. In practice, there are two options:
- We can use a famous algorithm called Expectation-Maximization (EM) that carries out training in two stages: (i) First, calculate expected probabilities for points belonging to specific components. (ii) Second, update parameters of components. We will not discuss this algorithm here since we are lazy deep-learning bastards. However, I highly recommend looking the details of the EM algorithm up in one the textbooks (e.g., (Bishop, 2006), (Barber, 2012) or (Murphy, 2012)), and implement it.
- The optimization can be done using gradient-based methods.
Here, we follow the second path because it is easier since we can use any library with autograd. The procedure is straightforward: Calculate gradients of the log-likelihood with respect to the paramters and update the parameters. That is all! The only thing we need to remember is to use the LSE function.
Some examples of fitting a mixture of Gaussians (for different numbers of components) to the half-moon data is presented in Figure 5. As you can notice, my curious reader, fitting too few components (Figure 5.A) results in a very poorly generalizable model, while taking too many components could lead to numerical instabilities (e.g., if a component is located on a datapoint and the variance collapses to $0$). In general, taking more components (e.g., see Figre 5.D) results in a better fit and a better log-likelihood value. Touching upon this topic, sometimes we need a regularization of some sort, but we will not discuss it further. You can read about it, my curious reader, in one of the textbooks (e.g., about a Bayesian treatment of a mixture of Gaussians (Bishop, 2006)).
A

B

C
D

Other mixture models Here, we discussed mixtures of Gaussians, however, we can formulate any mixture model, depending on the character of observable data. For instance, for binary data, we get a mixture of Bernoullis:
\begin{equation} p(x; \theta) = \sum_{k=1}^{K} \pi_k \mathrm{Bern}(x | \theta) . \end{equation}
Similarly, we can build other mixture models. In general, building a mixture of distribution from the exponential family of distributions is straightforward due to the fact that we can puse the LSE trick to formulate tractable the log-likelihood-based training objective.
Coding Mixture of Gaussians (MoG)¶
Alright, my curious reader, it is enough of a chit-chat. I know you, and I feel you, we should code a MoG up! We will train our MoG on a simple data (tiny handwritten images). Some examples are presented in Figure 6. These are not necessarily complicated, and very small, but still training a model to generate such objects is non-trivial, as we will see.

But back to work! An implementation of an MoG is presented in the code snippet below. Please take a careful look, my curious reader, and try to understand every single line. For instance, we use Gaussian components parameterized with means and diagonal covariance matrices (in fact, we use log-variances for numerical convenience). Moreover, we allow two options for component probabilities: $\omega$'s are either trainable or fixed and equiprobable, i.e., $\omega_k = \frac{1}{K}$ for all $k=0, \ldots, K-1$. Note that we must keep $\sum_k \omega_k = 1$ and each $\omega_k \in [0, 1]$. If we train $\omega$'s with a gradient-based method, it is hard to ensure that. Therefore, we introduce parameters $w$'s in the code and then use the softmax function to turn them into $\omega$'s. A simple trick that always works.
Alright, we are good to go. Buckle up and code it up!
class MoG(nn.Module):
def __init__(self, D, K, uniform=False):
super(MoG, self).__init__()
print('MoG by JT.')
# hyperparams
self.uniform = uniform
self.D = D # the dimensionality of the input
self.K = K # the number of components
# params
self.mu = nn.Parameter(torch.randn(1, self.K, self.D) * 0.25 + 0.5)
self.log_var = nn.Parameter(-3. * torch.ones(1, self.K, self.D))
if self.uniform:
self.w = torch.zeros(1, self.K)
self.w.requires_grad = False
else:
self.w = nn.Parameter(torch.zeros(1, self.K))
# other
self.PI = torch.from_numpy(np.asarray(np.pi))
def log_diag_normal(self, x, mu, log_var, reduction='sum', dim=1):
log_p = -0.5 * torch.log(2. * self.PI) - 0.5 * log_var - 0.5 * torch.exp(-log_var) * (x.unsqueeze(1) - mu)**2.
return log_p
def forward(self, x, reduction='mean'):
# calculate components
log_pi = torch.log(F.softmax(self.w, 1)) # B x K, softmax is used for R^K -> [0,1]^K s.t. sum(pi) = 1
log_N = torch.sum(self.log_diag_normal(x, self.mu, self.log_var), 2) # B x K, log-diag-Normal for K components
# =====LOSS: Negative Log-Likelihood
NLL_loss = -torch.logsumexp(log_pi + log_N, 1) # B
# Final LOSS
if reduction == 'sum':
return NLL_loss.sum()
elif reduction == 'mean':
return NLL_loss.mean()
else:
raise ValueError('Either `sum` or `mean`.')
def sample(self, batch_size=64):
# init an empty tensor
x_sample = torch.empty(batch_size, self.D)
# sample components
pi = F.softmax(self.w, 1) # B x K, softmax is used for R^K -> [0,1]^K s.t. sum(pi) = 1
indices = torch.multinomial(pi, batch_size, replacement=True).squeeze()
for n in range(batch_size):
indx = indices[n] # pick the n-th component
x_sample[n] = self.mu[0,indx] + torch.exp(0.5*self.log_var[0,indx]) * torch.randn(self.D)
return x_sample
def log_prob(self, x, reduction='mean'):
with torch.no_grad():
# calculate components
log_pi = torch.log(F.softmax(self.w, 1)) # B x K, softmax is used for R^K -> [0,1]^K s.t. sum(pi) = 1
log_N = torch.sum(self.log_diag_normal(x, self.mu, self.log_var), 2) # B x K, log-diag-Normal for K components
# log_prob
log_prob = torch.logsumexp(log_pi + log_N, 1) # B
if reduction == 'sum':
return log_prob.sum()
elif reduction == 'mean':
return log_prob.mean()
else:
raise ValueError('Either `sum` or `mean`.')
The full code can be found here: [Link]. After running our MoG with $K=25$ and trainable components probabilities, we should obtain results like in Figure 7. A few notes here:
- The generated images are not fantastic (Figure 7A), however, they resemble images (if you close your eyes a bit, perhaps). The point here is not to get state-of-the-art; we are here to learn the principles. If you wish to get better results, go ahead and play with the code!
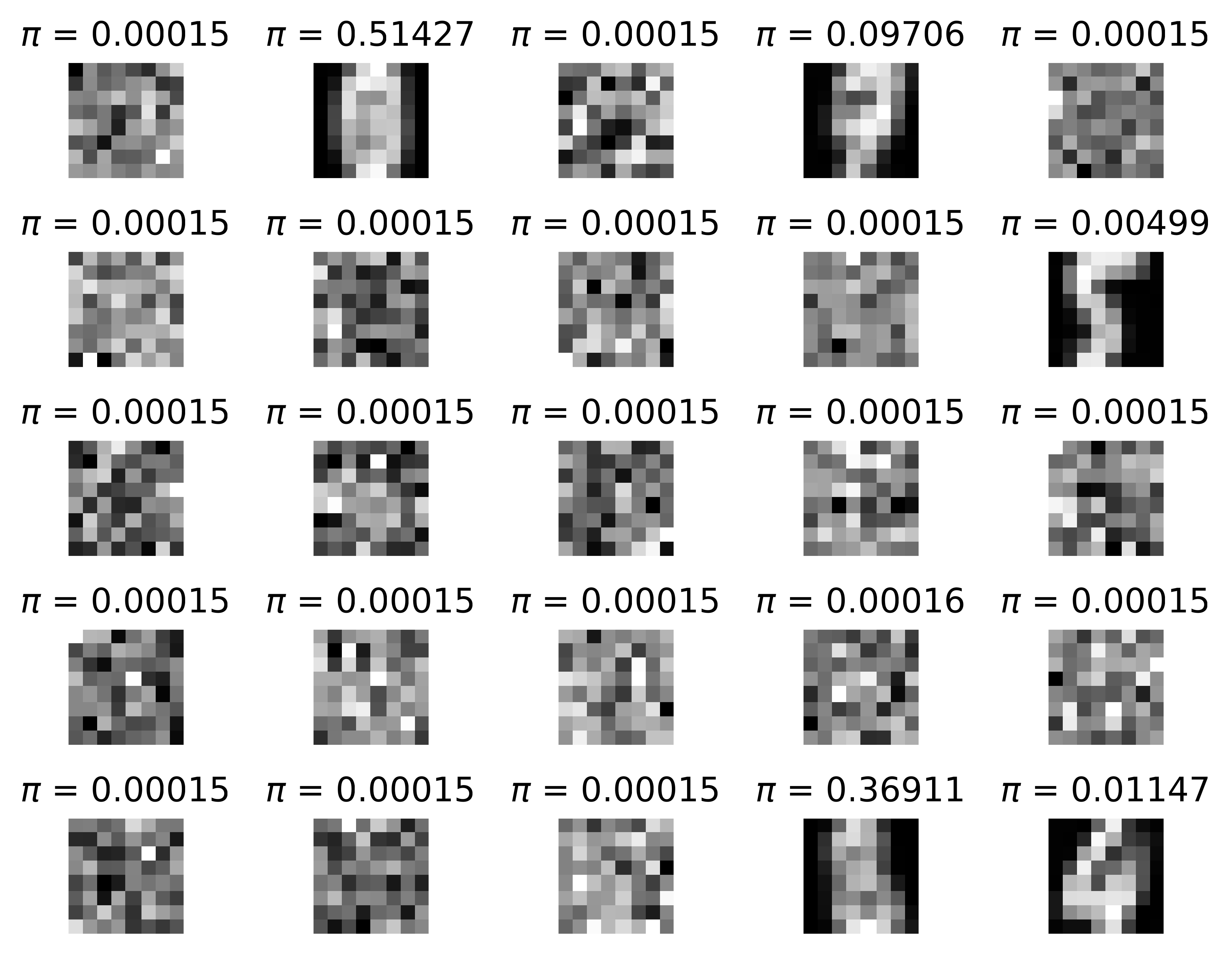
- Take a look at the means (Figure 7B)! It is really interesting what happens there. First, there are many collapsed components for which $\omega_k$ is close to $0$ (component probabilities are presented above each mean in Figure 7B). This means that they are basically useless and we could even remove them from the mixture model. Second, the components with non-zero probability are either quite specific (e.g., a component for $5$'s or $4$'s) or very generic (e.g., the two means with high $\omega$'s).
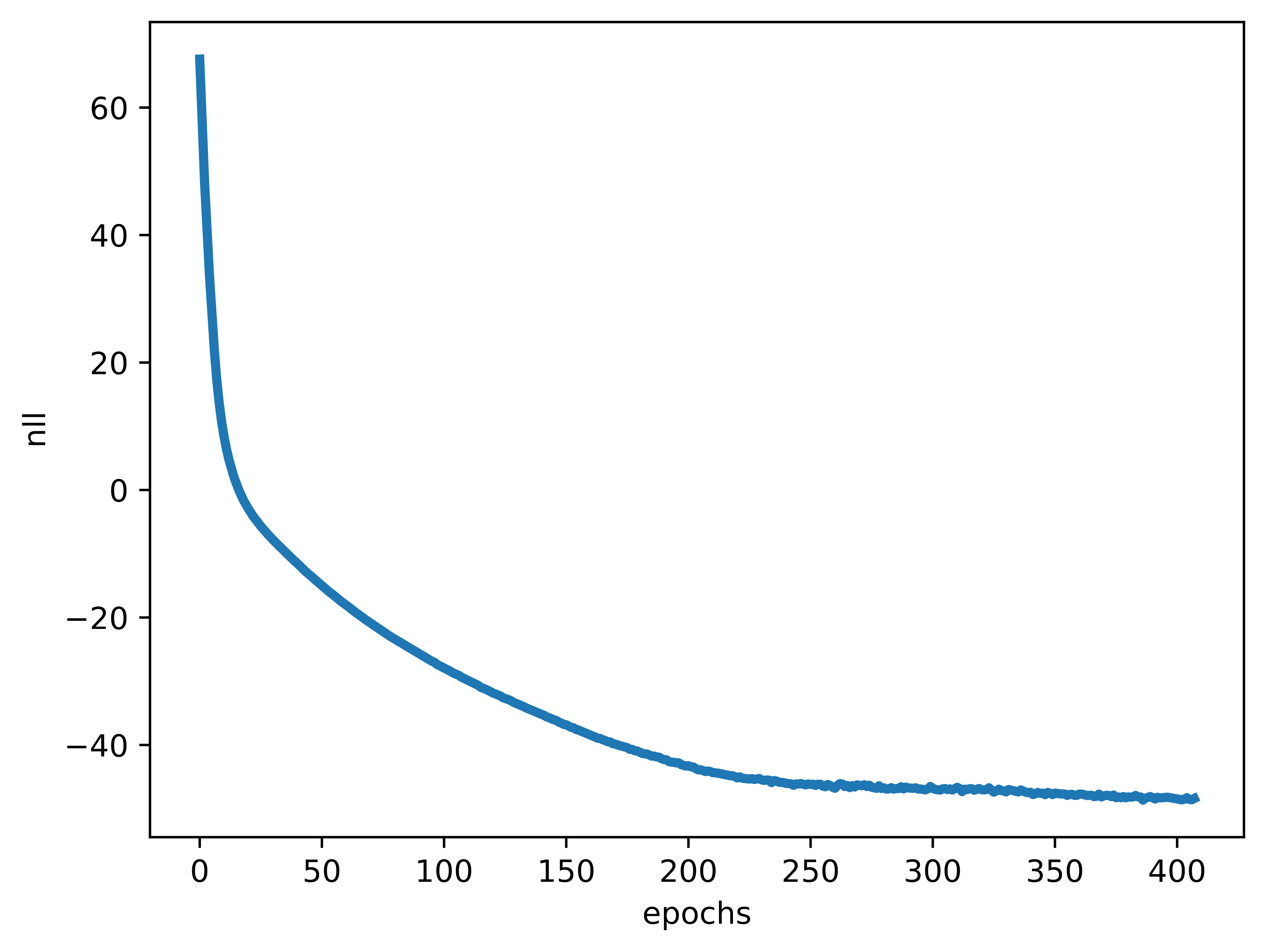
- The training is very smooth and stable (see Figure 7C). The negative log-likelihood is dropping nicely. However, it does not mean we should not use additional tricks and/or play with hyperparameter values to get even better results! Please remember, my curious reader, never be fooled with a nicely-looking curves or loss values in Generative AI. Always try to inspect what is generated by your model.
- Please be aware that the solution we found here is local, not global! It means that there exist multiple non-collapsed solutions and finding the best one (global) is hard if not (almost) impossible. Moreover, if a component collapses (i.e., $\sigma_k^2 = 0$), then we get the unbounded likelihood. To mitigate this issue, one can add a regularization term (Mattei & Frellsen, 2018).
A

B
C
There is more than mixture models, e.g., hierarchical mixture models (a.k.a. Probabilistic Circuits)¶
Mixture models are latent variables models (since we have latent variables representing component numbers). Here, we discuss finite mixture models with $z$ being a categorical variable. There are also infinite mixture models with $z$ being continuous, for example. We will look into those models on another occasion. Moreover, the presented mixture models are not very deep since there is only a single level of latent variables. In the following, we will briefly look into a very broad class of hierarchical mixture models: Probabilistic Circuits. Before we do that, we will say a few words about the simplest model possible, namely, fully-factorized models.
Fully-factorized models¶
An MoG is a quite powerful model that allows calculating the evidence. However, calculating MAP for MoGs is intractable because:
\begin{align} \max_{x} p(x) &= \max_{x} \sum_{k} \omega_k p_{k}(x) \\ &\neq \sum_{k} \max_{x} \omega_k p_{k}(x) , \end{align}in other words, we cannot swap the sum and the max.
However, if we take a very simple model that is fully-factorized (i.e., all varianbles are stochastically independent from each other):
\begin{equation} p(\mathbf{x}) = \prod_{i} p_i(x_i), \end{equation}then calculating EVI, MAR and MAP is linear! But it is not very expressive... However, here is a question: Can we combine somehow a mixture model and a fully-factorized model to get the best of the two worlds? The answer is... YES!
Hierarchical mixture models: Probabilistic Circuits¶
Building blocks Let us introduce the following semantics (Vergari et al., 2021):
- Nodes correspond either to distributions or an operation (a summation or a product);
- Edges define directions of probability flows;
- Inputs to nodes are random variables (their values) or probabilities;
- Outputs are probabilities.
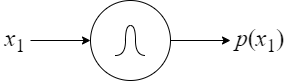
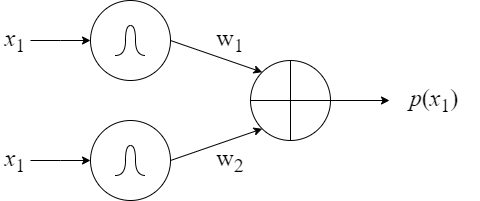
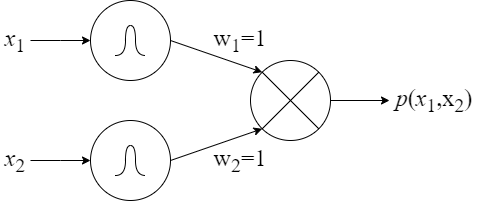
Further, we formulate the following basic units (see Figure 8):
- a base unit (Figure 8A): the input is a value of a random variable and the output is its probability (in other words, this unit implements a probability distribution);
- a sum unit (Figure 8B): inputs are values of a random variable and the output is a probability of a mixture model;
- a product unit (Figure 8C): inputs are values of different random variables and the output is a probability of a fully-factorized distribution.
A
B
C
To build tractable probability distributions out of these units, we need to impose a few constraints:
- Decomposability: A product unit is decomposable if its children depend on disjoint sets of variables.
- Smoothness: A sum unit is smooth if its children depend of the same variables.
Fulfilling these two constraints give us tractable MAR and CON (for tractable MAP we need other properties, see (Choi et al., 2020) for details).
Probabilistic Circuits Now we have simple building blocks that define proper distributions. Similarly to neural networks, we can build complex distributions that, in fact, define hierarchical mixture models (i.e., mixtures of mixtures of ... and so on). In principle, for sufficiently large $K$, a mixture model can model any distribution. However, we know that if $K > N$ (i.e., there are more components than datapoints), the model collapses and is not generalizable. Therefore, having a hierarchical mixture model could help to keep expresivness while increasing generalizability. In Figure 9, we present a few examples of Probabilistic Circuits (PCs) consisting of the simple building units.
An example We quickly present nice properties of PCs based on an example presented in a fantastic tutorial (Vergari et al., 2020). If you are interested in PCs, this is a great start for you, my curious reader! Here, we briefly present the power of PCs!
Let us say that we have a PC like in Figure 10.A, defining the probability distribution over four random variables, $p(x_1, x_2, x_3, x_4)$, in which all base units are known distributions. Our goal is to calculate a marginal distribution $p(x_2, x_4)$. How to do that then? It is easy and requires the following procedure:
- For variables we marginalize over, we set the values of based units to $1$ (green nodes in Figure 10.B).
- For given values of $x_2$ and $x_4$, we calculate the probabilities (orange nodes in Figure 10.C).
- We carry out a feedforward (bottom-up, i.e., from all leaves to the root) evaluation of all units.
The final value of the MAR distribution for given values of $x_2$ and $x_4$ is in the root. The beauty of PCs is that all operations are tractable, they are very basic and the final result is given in time linear in circuit size!
Final comments on PCs The world of PCs is very rich and gets extra traction nowadays, mainly due to their tractability. Here are some useful pointers and thoughts:
- PCs are closely related to logical circuits (Darwiche & Marquis, 2002). For instance, sum units can be seen as probabilistic generalizations of OR units while products units are closely related to AND units.
- If we know the architecture of PCs, training (i.e., estimating parameters of base units) can be accomplished by applying Expectation-Maximization (Desana Schnörr, 2016; Peharz et al., 2016) or a gradient-based method (Peharz et al., 2020).
- Learning a PC structure from data is more challenging and typically require additional constraints or assumptions (Gens & Domingos, 2013).
- There are specialized packages and repos that can help you to build and learn PCs, e.g., Einsum Networks in PyTorch (Peharz et al., 2020), Juice in Julia (Dang et al., 2021), SPFlow in Python (Molina et al., 2019).
- Interestingly, PCs could generalize well-known methods like Decision Trees or Random Forests. In (Correia et al., 2020) it was shown that Decision Trees and Random Forests can be turned into PCs and, additionally, treated as generative models!
I give only a tiny-weeny piece of a fantastic world of PCs here! I hope you got interested, my curious reader, and you will delve further into this class of deep (hierarchical), tractable probabilistic models.
References¶
(Barber, 2012) Barber, D. (2012). Bayesian reasoning and machine learning. Cambridge University Press.
(Bishop, 2006) Bishop, C. M. (2006). Pattern recognition and machine learning. Springer
(Choi et al., 2020) Choi, Y., Vergari, A., & Van den Broeck, G. (2020). Probabilistic circuits: A unifying framework for tractable probabilistic models. UCLA. URL: http://starai. cs. ucla. edu/papers/ProbCirc20. pdf, 6.
(Correia et al., 2020) Correia, A., Peharz, R., & de Campos, C. P. (2020). Joints in random forests. Advances in neural information processing systems, 33, 11404-11415.
(Dang et al., 2021) Dang, M., Khosravi, P., Liang, Y., Vergari, A., & Van den Broeck, G. (2021, May). Juice: A julia package for logic and probabilistic circuits. In Proceedings of the AAAI Conference on Artificial Intelligence (Vol. 35, No. 18, pp. 16020-16023).
(Darwiche & Marquis, 2002) Darwiche, A., & Marquis, P. (2002). A knowledge compilation map. Journal of Artificial Intelligence Research, 17, 229-264.
(Desana Schnörr, 2016) & Desana, M., & Schnörr, C. (2016). Learning arbitrary sum-product network leaves with Expectation-Maximization. arXiv preprint arXiv:1604.07243.
(Gens & Domingos, 2013) Gens, R., & Domingos, P. (2013). Learning the structure of sum-product networks. In International conference on machine learning (pp. 873-880). PMLR.
(Koller & Friedman, 2009) Koller, D., & Friedman, N. (2009). Probabilistic graphical models: principles and techniques. MIT press.
(Mattei & Frellsen, 2018) Mattei, P. A., & Frellsen, J. (2018). Leveraging the exact likelihood of deep latent variable models. Advances in Neural Information Processing Systems, 31.
(Molina et al., 2019) Molina, A., Vergari, A., Stelzner, K., Peharz, R., Subramani, P., Di Mauro, N., Poupart, P. and Kersting, K. (2019). SPFlow: An easy and extensible library for deep probabilistic learning using sum-product networks. arXiv preprint arXiv:1901.03704.
(Murphy, 2012) Murphy, K. P. (2012). Machine learning: a probabilistic perspective. MIT press.
(Peharz et al., 2016) Peharz, R., Gens, R., Pernkopf, F., & Domingos, P. (2016). On the latent variable interpretation in sum-product networks. IEEE transactions on pattern analysis and machine intelligence, 39(10), 2030-2044.
(Peharz et al., 2020) Peharz, R., Lang, S., Vergari, A., Stelzner, K., Molina, A., Trapp, M., Van den Broeck, G., Kersting, K. and Ghahramani, Z. (2020). Einsum networks: Fast and scalable learning of tractable probabilistic circuits. In International Conference on Machine Learning (pp. 7563-7574). PMLR.
(Vergari et al., 2020) Vergari, A., Choi, Y., Peharz, R., & Van den Broeck, G. (2020). Probabilistic circuits: Representations, inference, learning and applications. In Tutorial at the The 34th AAAI Conference on Artificial Intelligence.
(Vergari et al., 2021) Vergari, A., Choi, Y., Liu, A., Teso, S., & Van den Broeck, G. (2021). A compositional atlas of tractable circuit operations for probabilistic inference. Advances in Neural Information Processing Systems, 34, 13189-13201.