Large Language Models (LLMs)¶
What are Large Language Models (LLMs)?¶
Introduction How is it possible, my curious reader, that we can share our thoughts? How can it be that we discuss generative modeling, probability theory, or other interesting concepts? How come? The answer is simple: Language. We communicate because the human species developed a pretty distinctive trait that allows us to formulate sounds in a very complex manner to express our ideas and experiences. At some point in our history, some people realized that we forget, we lie, and we can shout as strongly as we can but we will not be understood farther than a few hundred meters. The solution was a huge breakthrough: Writing. This whole mumbling on my side here could be summarized using one word: Text. We know how to write (and read) and we can use the word "text" to mean "language" or "natural language" to avoid any confusion with artificial languages like Python or formal language.
Communication is an essential component of our lives. Therefore, it is no surprise that processing text, or natural language in general, attracted a lot of attention from day one of AI. Since the 50s of the twentieth century, people have been fascinated by the possibility of building communicating bots. Thanks to Alan Turing, we have even a famous test named after him which states that if a machine can "talk" to a human being without being recognized as a machine, then we can call it "intelligent". The first chatbot was even introduced in the 60s of the twentieth century. ELIZA, because it was its name, was able to match patterns and mimic an "intelligible" conversation. But it was way far from being "intelligent" and, after all, it was unable to generate responses that would fool good Dr. Turing. It took us over 60 years (nothing in the history of human beings but eons in the history of AI) to get to the point where we can debate about intelligence, originality, novelty, and many other aspects that were exclusive to us, humans. And all these are possible due to generative modeling.
Obviously, we communicate not only using text, but also images, audio, diagrams, and all sorts of "languages" (e.g., chemical reactions, mathematics). That is why, multimodality plays a crucial role in developing the next level of AI systems. In the following, we will talk about natural language processing (NLP) and how it was influenced by deep learning. The combination of deep learning and NLP gave rise to their baby called a Large Language Model (LLM). Eventually, we will outline how LLMs have changed our way of thinking about AI systems. As a result, we will talk about Generative AI systems (GenAISys).
Oh, and before we start, LLM is not equivalent to Generative AI. Generative AI is about all modalities, and LLMs are about processing some language. I am not a "term nazi", I am really flexible, but it is quite sad that experts nowadays repeat this nonsense. It is hurtful for the field and the industry. Alright, enough of being an old prick and let us delve into LLMs and GenAISys!
Natural Language Processing and Deep Learning Natural Language Processing (NLP) is the field that focuses on building machines that can manipulate human language. NLP aims at developing methods and techniques for processing written language (i.e., text). The tasks of NLP vary from text classification (e.g., sentiment analysis, spam detection), text correction (e.q., grammatical error correction), machine translation (e.g., translating using sequence-to-sequence models a.k.a. seq2seq), semantic analysis (e.g., topic modeling), text generation (e.g., chatbots), text summarization, named entity recognition (NER), information retrieval (IR) to question answering and chatbots. The main question though in NLP is about how to represent text such that it is useful for downstream tasks.
Classical NLP methods focused a lot on syntactic, i.e., grammar and sentence structures (Chomsky 1965). However, semantics is extremely important for proper communication and this remained a challenge for a long time. The first attempts to grasp the meaning of a piece of text relied on formulating tokenizers, specialized modules that represented text in a machine-readable manner. The first tokenizers counted words (so-called bag-of-words) in a document or an n-gram (a sequence of n words), giving rise to a numerical representation of text. However, such a representation is dependent on the document length, therefore, it seems more appropriate to look at normalized quantities like term frequency (tf), namely, the number of occurrences of a word in a document divided by the number of words in a document, and inverse document frequency (idf) that corresponds to the importance of a term in the whole corpus, calculated as the logarithm of the number of documents in the corpus divided by the number of documents that include the term. Typically, the tf-idf representations are used. These representations provide a lot of information about documents and can be easily manipulated by machines. However, they are pretty limited due to chosen n-grams and heavily depend on the available corpus of documents. Simpler tokenizers replace characters (or n-grams of characters) with integers such that text could be treated as a sequence of numbers. These tokenizers do not provide any meaning of text but play a crucial role in contemporary NLP methods, as we will see shortly.
I think you feel what is coming, my curious reader. I can almost read your mind. What are you whispering? It would be amazing to have a method that can learn semantics from data. And, ideally, by applying neural networks? You are right! The big breakthrough in NLP came with the Word2Vec method (Mikolov et al., 2013) which allowed learning word embeddings from raw text by using neural networks for a given context. In some sense, this paper opened Pandora's box (but in a good sense) that led to the development of Language Models parameterized by neural networks. Since these neural networks consisted of millions of weights, and later on (and nowadays) even of billions of weights, many researchers and practitioners have started calling them Large Language Models to distinguish them from more classical language models.
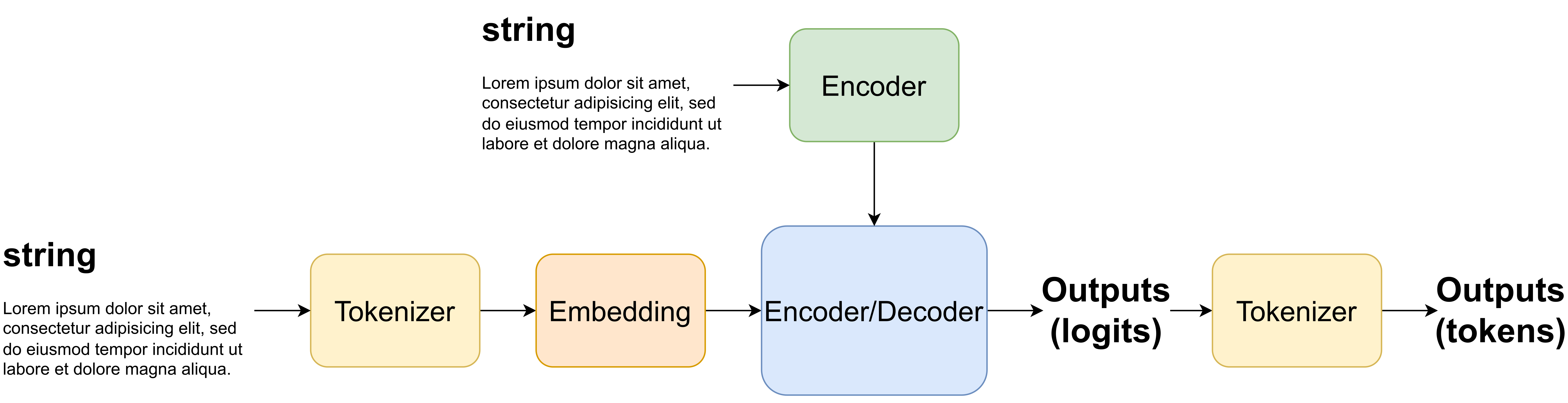
General architectures of LLMs Before we talk more about details like how to parameterize LLMs (i.e., what kind of neural networks to use) and how to learn them, let us briefly discuss their general architectures. No matter what, each LLM requires a tokenizer to turn text into numbers (e.g., integers), and an embedding that changes them eventually to real-valued vectors. Sometimes, both modules are treated as one (e.g., vectorizers in scikit-learn). A popular choice for a tokenizer these days is byte pair encoding which greedily merges commonly occurring sub-strings based on their frequency (Gage, 1994). The embedding module serves only a single purpose, namely, to map a token represented as a one-hot vector to a real-valued vector of size $D$. Then, after processing embeddings using a neural network, the output must be de-tokenized to a string again.
In general, we can distinguish three types of LLMs:
- Encoders: These LLMs take a piece of text (string) and return an encoding, i.e., a numerical representation of the input. Encoders can have access to the whole input at any point of processing and they do not require any specific constraints. They provide outputs in a single forward run both during training and at the inference time.
- Decoders: This class of LLMs is pretty specific because they are used for generating new texts. They can be seen as autoregressive models and, as such, neural networks used to parameterize them must be causal. For decoders, the sampling procedure is an iterative process, thus, it is typically very slow.
- Encoder-Decoders and Encoder-Encoders: LLMs can be conditional and then we need to combine an encoder processing a conditioning, and an encoder or a decoder that provides an encoding of input text or generates new text, respectively.
In Figure 1.A, you can see a schematic representation of an encoder or a decoder, and in Figure 1.B there is an encoder-encoder(decoder) presented. Now the question is how to parameterize LLMs.
A

B
Parameterizations The key component of any LLM is its parameterization. No matter if it is an encoder or a decoder, it is large because it uses hierarchical, (very) deep neural networks. But we cannot just use any neural network because we deal with text (i.e., sequences). As a result, a neural network must process vectors and, for decoders, output new text in the so-called causal manner (i.e., without looking "into the future").
If we go back to autoregressive models, we know that we can use recurrent neural networks (RNNs) and convolutional layers (CNNs) for processing text. RNNs seem to fit perfectly language modeling due to their intrinsic sequential structure. They were used by (Mikolov et al., 2010) to formulate one of the first RNN-based decoders and then RNN-based encoder-decoders (Cho et al., 2014). As shown in (Jozefowicz et al., 2016), the combination of CNNs and RNNs indicated an improvement in terms of language modeling. However, this was no surprise because the first successful encoders were based entirely on convolutional layers (Kalchbrenner et al., 2014) before they were used for decoders (Dauphin et al., 2017) and encoder-decoders (Kalchbrenner et al., 2016). However, RNN-based and CNN-based language models either suffered from forgetting or scaling issues.
The big breakthrough in LLMs has come with the introduction of transformers (Vaswani et al., 2017) and their utilization of (multi-head) attention layers. In all fairness, transformers proposed a few important implementation tricks, such as multi-head attention to learn multiple patterns in input tokens, layer normalization for preventing gradient blowing, and positional embeddings to ensure that tokens are treated as sequences and not as a set of tokens. Transformers turned out to be great at scaling up models, resulting in models with billions of weights. However, transformers require quadratic time and quadratic memory in the number of tokens (however, with Flash Attention (Dao et al., 2022) it becomes linear).
Recently, many people working on LLMs have focused on making them leaner (we can refer to those models as L3M: Lean Large Language Models). There are three main aspects to obtain L3M: (i) quantization of LLMs (i.e., fewer bits per weight that leads to less physical memory on disc), (ii) faster training, (iii) faster inference.
Quantization is a long-standing problem in deep learning and it poses new challenges for various architectures. For transformers, there have been a lot of successes like quantization aware training with modified self-attention (Bondarenko et al., 2024). Recently, it was shown that using transformers with weights of linear layers taking values in $\{-1, 0, 1\}$ results in leaner methods (around $\times 3$ lower memory requirements and around $\times 2$ lower latency in ms) while achieving comparable performance as float16 models.
For faster training/inference, there were various methods proposed. For instance, FlashAttention focused on speeding up attention layers by accounting for I/O operations (reads and writes) between different levels of GPU memory (Dao et al., 2022). A different approach rephrases the attention mechanism using a linear dot-product of kernel feature maps. The resulting linear transformer (Katharopoulos et al., 2020) makes further use of the associativity property of matrix products to reduce the quadratic complexity to linear complexity in the big-O notation of the length of the input sequence. However, a transformer-based language model is not all we need (and have)! There are other classes of LLMs that operate like RNNs at inference time and are fully parallelizable during training. Selective State Space Models (S4Ms) are built on top of state space models, i.e., a linear dynamical system with hidden variables/states (Gu et al., 2021). The adverb "selective" comes from the fact that S4Ms use an attention mechanism. One of the extensions of S4Ms, Mamba (Gu & Dao, 2023), outperformed some transformers. Other S4M-inspired models like Retentive Networks (RetNets) (Sun et al., 2023) or RWKV (Peng et al., 2024) successfully compete with the largest transformer-based models while maintaining linear training complexity and constant inference complexity. An interesting LLM, Jamba (Lieber et al., 2024), is a combination of Mamba layers with transformer layers. Taking a hybrid approach poses a promising future direction.
Another important extension of current LLMs is based on the idea of Mixture-of-Experts (MoE) (Fedus et al., 2022), a concept well-known in machine learning (Jacobs et al., 1991). Instead of learning a single model, we train multiple LLMs (experts) that can specialize in certain topics. Then, for given input tokens, a router selects multiple experts and the final outcome is calculated as a weighted average of the outcomes given by th experts. An example of an implementation of an MoE-LLM is Mixtral-of-Experts (Jiang et al., 2024).
An overview of various parameterizations of LLMs is presented in Table 1.
| Architecture | Inference: Time | Inference: Memory | Parallel | Training: Time | Inference: Memory |
|---|---|---|---|---|---|
| RNNs | $O(1)$ | $O(1)$ | NO | $O(N)$ | $O(N)$ |
| Transformer | $O(N)$ | $O(N)$ | YES | $O(N^2)$ | $O(N)$ |
| Linear Transformer | $O(1)$ | $O(1)$ | YES | $O(N)$ | $O(N)$ |
| S4M | $O(1)$ | $O(1)$ | YES | $O(N\log N)$ | $O(N)$ |
| RWKV/RetNet/Mamba | $O(1)$ | $O(1)$ | YES | $O(N)$ | $O(N)$ |
Learning As you can imagine, my curious reader, training of LLMs is probably something a bit more complicated than just LMs (or other models, especially the small ones). The answer is yes and no. No because, after all, they are models that either encode or generate, so nothing we have not dealt with. Yes because LLMs are large and we need a lot of data. Very often LLMs are seen as foundation models (FMs) (Bommasani et al., 2021) that assume two phases of training:
- Pre-training: This is the initial stage that aims at preparing an LLM for further tasks. A model is trained either using the masked loss, $\ell_{\text{masked}}(\theta) = - \mathbb{E}_{\mathbf{x} \sim p_{\text{data}}(\mathbf{x})} \mathbb{E}_{M}\Big[ \sum_{m \in M} \ln p_{\theta}(x_{m} \mid {\mathbf{x}}_{-m}) \Big]$, where $M$ indicates which tokens should be dropped from $\mathbf{x}$ and the goal is to reconstruct masked tokens, or by minimizing the negative log-likelihood $\ell_{\text{gen}}(\theta) = - \mathbb{E}_{\mathbf{x} \sim p_{\text{data}}(\mathbf{x})} \Big[ \ln p_{\theta}(\mathbf{x}) \Big]$. The masked loss is used for encoders while the negative log-likelihood is typically utilized by decoders. The pre-training stage involves a lot (and I really mean "a lot"!) of data because the goal of this stage is to train general patterns in data, e.g., grammar and co-occurrences of words, or a specific programming language.
- Fine-tuning: A pre-trained model is further specialized on another dataset for a downstream task. For instance, an LLM can be trained on specific data, e.g., legal data to generate legal documents or a new programming language. However, the LLM can be also fine-tuned to carry out other tasks like text summarization, Q&A, text classification, sentiment analysis, etc. Depending on the task at hand, the LLM is optimized either using $\ell_{\text{masked}}(\theta)$ or $\ell_{\text{gen}}(\theta)$, or serves as a starting point for a new LLM for another task. In the former case, we typically optimize a different objective with an additional neural network, $\ell_{\text{pred}}(\theta, \phi) = - \mathbb{E}_{\mathbf{x},y \sim p_{\text{data}}(\mathbf{x}, y)} \left[ \ln p_{\theta, \phi}(\mathbf{x}, y) \right]$.
These two steps are quite general and fully depend on a given task at hand. For instance, the first Generative Pretrained Transformers (GPTs) (Radford et al., 2018) were pre-trained using the negative log-likelihood or they were initialized by training with the masked loss like in Bidirectional Encoder Representations from Transformers (BERT) (Devlin et al., 2018). Eventually, GPTs were fine-tuned with the negative log-likelihood loss. It is also possible to combine various losses, e.g., $\ell_{\alpha}(\theta) = \ell(\theta) + \alpha \ell_{\text{masked}}(\theta)$, which could be seen as a penalized negative log-likelihood objective. This idea was utilized in pre-training LLMs for various problems at once (Dong et al., 2019) or, with $\alpha=1$, for pre-training an LLM for molecules (Izdebski et al., 2023).
The problem with fine-tuning LLMs lies in the size of LLMs. Ideally, fine-tuning should be quick and cheap but it is hard to achieve if we deal with models with billions of weights. A possible solution is a technique known as Low-Rank Adaptation (LoRA) (Hu et al., 2021). The idea is relatively simple but crazily smart! Instead of updating a full-rank matrix of weights $\mathbf{W}$ (a side note: LoRA typically updates only attention matrices since they pose the greatest bottleneck), we introduce a new set of learnable matrices during fine-tuning, $\mathbf{A}$ and $\mathbf{B}$ while keeping $\mathbf{W}$ frozen. As a result, the forward pass looks as follows:
\begin{equation} \mathbf{h}_{l} = \mathbf{W}\mathbf{h}_{l-1} + \mathbf{B} \mathbf{A} \mathbf{h}_{l-1} . \end{equation}
Where does the whole magic come from then? From sizes of the matrices! If $\mathbf{W}$ is a $D \times d$ matrix, then $\mathbf{B}$ is a $D \times k$ matrix and $\mathbf{A}$ is a $k \times d$ matrix, where $k \ll d$. As a result, we have a knob in the form of the dimensionality $k$ that controls the number of weights in the matrices $\mathbf{A}$ and $\mathbf{B}$, while the resulting matrix $\mathbf{B} \mathbf{A}$ is of the same size as $\mathbf{W}$. As a result, after applying LoRA, only a small fraction of the original number of weights is updated during fine-tuning. Typically, enlarging an LLM with even fewer than $1\%$ of new trainable weights is enough to achieve the same results as if the whole LLM is fine-tuned.
Famous LLMs There is a plethora of LLMs, a few already mentioned here. I do not even dare to start pointing them out. In Table 2, I gather only (very subjectively!) selected LLMs.
| Name | Type | Size | Reference/Date |
|---|---|---|---|
| BERT | Encoder | 0.11B - 0.34B | (Devlin et al., 2018) |
| BioGPT | Decoder | 0.35B | (Luo et al., 2022) |
| BioGPT | Decoder | 0.35B | (Luo et al., 2022) |
| Claude-3 | Decoder | 20B - ~2000B | Mar 4, 2024 |
| Falcon | Decoder | 7B - 180B | (Almazrouei et al., 2023) |
| GPT-2 | Decoder | ~1.5B | (Radford et al., 2019) |
| GPT-3 | Decoder | ~175B | September, 2020 |
| GPT-4 | Decoder | ~1000B | March 14, 2023 |
| LLaMA-2 | Decoder | 7B - 70B | (Touvron et al., 2023) |
| LLaMA-3 | Decoder | 8B - 70B | April 18, 2024 |
| Mamba | Decoder | 3B | (Gu & Dao, 2023) |
| Mistral | Decoder | 7B | September 27, 2023 |
| Mixtral | Decoder | 8$\times$7B | (Jiang et al., 2024) |
| PaLM | Decoder | 8B - 540B | (Chowdhery et al., 2023) |
| RoBERTa | Encoder | 0.125B - 0.355B | (Liu et al., 2019) |
| RWKV-5 (Eagle) | Decoder | 0.4B - 7B | (Peng et al., 2024) |
| RWKV-6 (Finch) | Decoder | 1.6B - 3B | (Peng et al., 2024) |
| T5 | Encoder-Decoder | 0.06B - 11B | (Raffel et al., 2020) |
| XLNet | Decoder | 0.11B - 0.34B | (Yang et al., 2019) |
Coding up our teenyGPT¶
Ufff... it was a lot of text but what you can expect from a discussion about Large Language Models if not a lot of text? But without further ado, let us delve into some code! In the following, we will discuss our own GPT model we can call teenyGPT, an (extremely) tiny implementation of a decoder LLM. We focus on small dataset of newspaper headlines and a simple tokenizer working at a character level. Our data consist of the batch dimension, the number of tokens and the values, and our loss function is simply the negative log-likelihood.
class LossFun(nn.Module):
def __init__(self,):
super().__init__()
self.loss = nn.NLLLoss(reduction='none')
def forward(self, y_model, y_true, reduction='sum'):
# y_model: B(atch) x T(okens) x V(alues)
# y_true: B x T
B, T, V = y_model.size()
y_model = y_model.view(B * T, V)
y_true = y_true.view(B * T,)
loss_matrix = self.loss(y_model, y_true) # B*T
if reduction == 'sum':
return torch.sum(loss_matrix)
elif reduction == 'mean':
loss_matrix = loss_matrix.view(B, T)
return torch.mean(torch.sum(loss_matrix, 1))
else:
raise ValueError('Reduction could be either `sum` or `mean`.')
The essential component is the transformer block. We define them using the PyTorch implementation of multi-head attention layers.
class TransformerBlock(nn.Module):
def __init__(self, num_emb, num_neurons, num_heads=4):
super().__init__()
# hyperparams
self.D = num_emb
self.H = num_heads
self.neurons = num_neurons
# components
self.msha = nn.MultiheadAttention(embed_dim=self.D, num_heads=self.H, batch_first=True)
self.layer_norm1 = nn.LayerNorm(self.D)
self.layer_norm2 = nn.LayerNorm(self.D)
self.mlp = nn.Sequential(nn.Linear(self.D, self.neurons * self.D),
nn.GELU(),
nn.Linear(self.neurons * self.D, self.D))
def forward(self, x, causal=True):
# Multi-Head Self-Attention
x_attn, _ = self.msha(x, x, x, is_causal=causal, attn_mask=torch.empty(1,1), need_weights=False)
# LayerNorm
x = self.layer_norm1(x_attn + x)
# MLP
x_mlp = self.mlp(x)
# LayerNorm
x = self.layer_norm2(x_mlp + x)
return x
Finally, we need to define our teenyGPT with a forward pass for the transformer, and a sampling procedure. Additionally, we can define an auxiliary metric, top-1 reconstruction accuracy, which takes the most probable token and uses it to check whether it is the same as the input token.
class teenyGPT(nn.Module):
def __init__(self, num_tokens, num_token_vals, num_emb, num_neurons, num_heads=2, dropout_prob=0.1, num_blocks=10, device='cpu'):
super().__init__()
# Remember, always credit the author, even if it's you ;)
print('teenyGPT by JT.')
# hyperparams
self.device = device
self.num_tokens = num_tokens
self.num_token_vals = num_token_vals
self.num_emb = num_emb
self.num_blocks = num_blocks
# embedding layer
self.embedding = torch.nn.Embedding(num_token_vals, num_emb)
# positional embedding
self.positional_embedding = nn.Embedding(num_tokens, num_emb)
# transformer blocks
self.transformer_blocks = nn.ModuleList()
for _ in range(num_blocks):
self.transformer_blocks.append(TransformerBlock(num_emb=num_emb, num_neurons=num_neurons, num_heads=num_heads))
# output layer (logits + softmax)
self.logits = nn.Sequential(nn.Linear(num_emb, num_token_vals))
# dropout layer
self.dropout = nn.Dropout(dropout_prob)
# loss function
self.loss_fun = LossFun()
def transformer_forward(self, x, causal=True, temperature=1.0):
# x: B(atch) x T(okens)
# embedding of tokens
x = self.embedding(x) # B x T x D
# embedding of positions
pos = torch.arange(0, x.shape[1], dtype=torch.long).unsqueeze(0).to(self.device)
pos_emb = self.positional_embedding(pos)
# dropout of embedding of inputs
x = self.dropout(x + pos_emb)
# transformer blocks
for i in range(self.num_blocks):
x = self.transformer_blocks[i](x)
# output logits
out = self.logits(x)
return F.log_softmax(out/temperature, 2)
@torch.no_grad()
def sample(self, batch_size=4, temperature=1.0):
x_seq = np.asarray([[self.num_token_vals - 1] for i in range(batch_size)])
# sample next tokens
for i in range(self.num_tokens-1):
xx = torch.tensor(x_seq, dtype=torch.long, device=self.device)
# process x and calculate log_softmax
x_log_probs = self.transformer_forward(xx, temperature=temperature)
# sample i-th tokens
x_i_sample = torch.multinomial(torch.exp(x_log_probs[:,i]), 1).to(self.device)
# update the batch with new samples
x_seq = np.concatenate((x_seq, x_i_sample.to('cpu').detach().numpy()), 1)
return x_seq
@torch.no_grad()
def top1_rec(self, x, causal=True):
x_prob = torch.exp(self.transformer_forward(x, causal=True))[:,:-1,:].contiguous()
_, x_rec_max = torch.max(x_prob, dim=2)
return torch.sum(torch.mean((x_rec_max.float() == x[:,1:].float().to(device)).float(), 1).float())
def forward(self, x, causal=True, temperature=1.0, reduction='mean'):
# get log-probabilities
log_prob = self.transformer_forward(x, causal=causal, temperature=temperature)
return self.loss_fun(log_prob[:,:-1].contiguous(), x[:,1:].contiguous(), reduction=reduction)
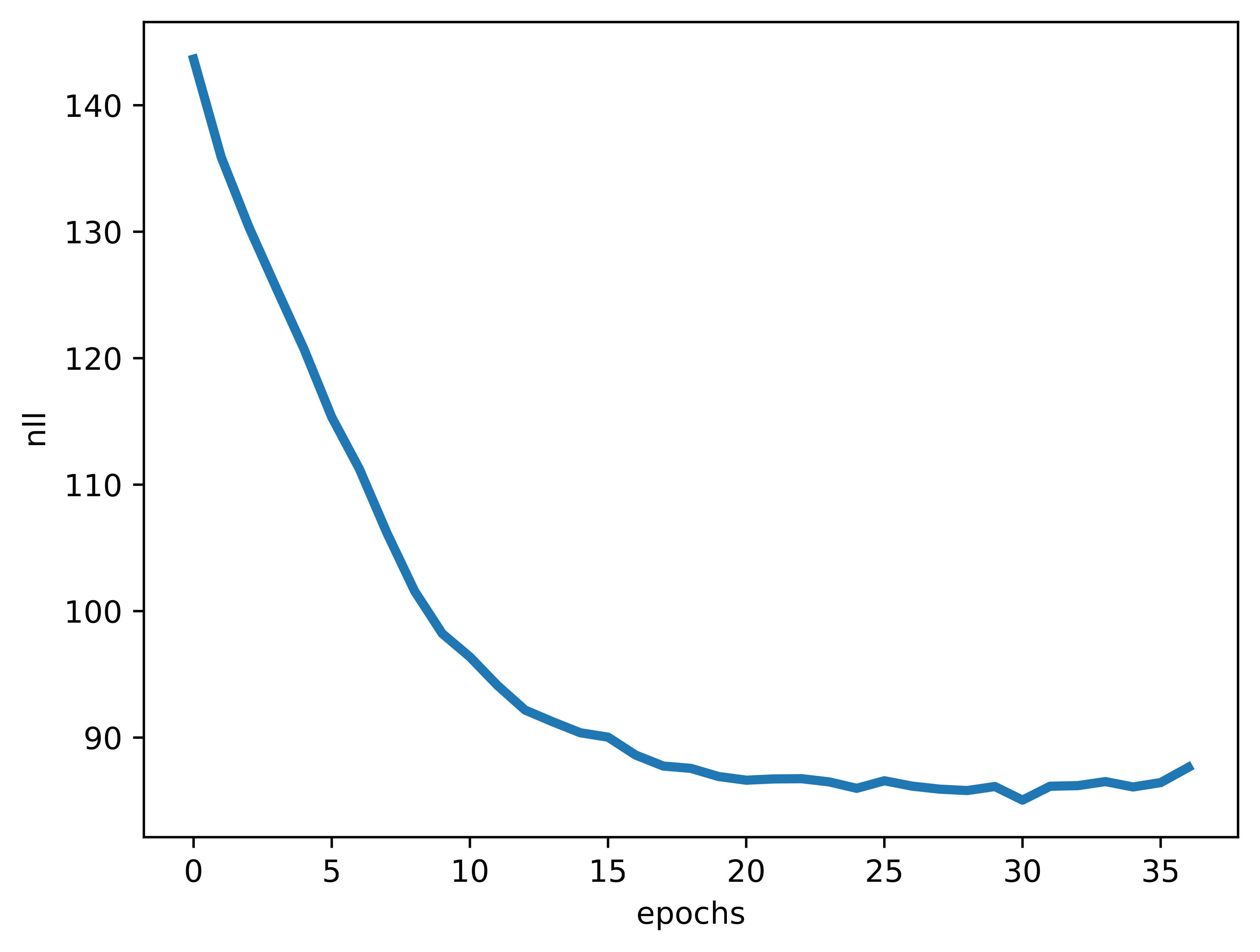
You can find the full code here: Link. For $128$ neurons in MLPs, $8$ attention heads, $4$ transformer blocks, and the embedding size equal $32$, we get a model with about $1$ million weights and the performance as in Figure 2.
A
B

C
| No. | Generation |
|---|---|
| 1 | british announces star market star market contract coronavirus case |
| 2 | british announces show announces set series |
| 3 | breaking say court coronavirus test positive |
| 4 | coronavirus death trump court star reade say say announcement say |
| 5 | coronavirus death test positive coronavirus case state state state state state state court |
| 6 | coronavirus case start star reade country test positive |
| 7 | british announces set coronavirus test positive |
| 8 | coronavirus case show death committee |
| 9 | michigan pro recovered country coronavirus test positive |
| 10 | coronavirus case star set state state state state state state state state allegation |
D
| No. | Generation |
|---|---|
| 1 | waterment share brand fabst dailey available hystering |
| 2 | pm rate murder test personn hirr kannish reported homeless tested decision |
| 3 | torotteney headlines sentencer everyone |
| 4 | milamican combinize give test pair catch attack |
| 5 | ugc harry first bitcoin boat wuhan chip man end masking precain |
| 6 | true fansed andrap new full forecasts |
| 7 | galaxy nigeria check police liverpool dam new deal threatens order |
| 8 | senator addeedly discharge tonie |
| 9 | grime everdille get improves reveals fan talk new revela false |
| 10 | uk coronavirus delivery due five aviversau despite return horror year |
As you can notice, my curious reader, the teeny LLM trains successfully, even with only a small amount of data, and around 1 million of weights! Comparing samples in Figure 2.C and Figure 2.D, we can clearly see that being too stochastic results in nonsensical headlines. However, overall, even though the model does not work perfectly, it learned to combine characters in such a way they constitute words (most of the time), and some headlines make even sense.
Other (selected) topics on LLMs¶
There are so many topics in LLMs at the moment, that it is nearly impossible to cover them all. In the following, I stress out some developments that are important and require a separate write-up but I leave these to others. Here are some highlights of the LLM community:
- Prompt Engineering: Prompt engineering is a bit tricky business and I mention it only for completeness of trendy topics in LLMs. However, my personal opinion is that prompt engineering is rather pseudo-engineering, a bunch of useful tricks for currently trained LLMs. From a practical point of view, it is useful to share commonly used practices on how to prompt an LLM. Nevertheless, in the long run, prompt engineering as we know it right now could be completely useless. Either way, my general advice is this: Prompt wisely, be precise, be nice (even though you talk to a machine!), instruct an LLM, and take whatever an LLM gives you with a pinch of salt. After all, LLMs are models and they can be (often are!) wrong.
- Instructing and Human Feedback: A big breakthrough in LLMs came with instructing them and giving them human feedback (Ouyang et al., 2022). The first model, a predecessor of ChatGPT, InstructGPT, was based on the idea of fine-tuning a GPT model using a dataset of rankings of model outputs provided by human evaluators. This approach was dubbed Reinforcement Learning from Human Feedback (RLHF) and during fine-tuning, first, a reward model is trained on the rankings, and then the reward model is used to assess generations according to the Proximal Policy Optimization (PPO) algorithm (Schulman et al., 2017). Later on, it was noticed that there is no need to train a separate reward model as a proxy to a human evaluator but it is possible to formulate the probability of preference of one generation over the other by using the LLM itself. This is the idea (and math, a really neat math) behind Direct Preference Optimization (DPO) (Rafailov et al., 2024).
- In-context learning: A great and fascinating capability of LLMs is so-called in-contet leraning (Dong et al., 2022). The idea relies on providing a few examples in the prompt to an LLM together with a query so that the LLM can figure out the answer from a very limited amount of data. To strengthen the LLM to be capable of in-context learning, it is important to cultivate it during training (e.g., during fine-tuning).
- Knowledge Graphs + LLMs: Knowledge Graphs (KGs) present a way of structuring data and relationships among them. However, their main drawbacks are lack of generalizability (if facts are missing, KGs are unable to provide any sort of approximate solution), and lack of language understanding. An enhancement of KGs with LLMs, or LLMs with KGs presents an interesting solution since LLMs are flexible but they lack proper grounding in facts (Pan et al., 2024).
- Adversarial attacks: Similarly to images, it is also possible to formulate adversarial attacks for LLMs (Zou et al., 2023). By proper prompting, it is possible to retrieve information that could be harmful to others, but also to obtain original training data (e.g., personal data).
- LLMs beyond text: There are multiple LLMs for other kinds of languages. For instance, programming languages are a perfect fit for training your own coding tools for enhancing programmers. Thanks to Generative AI, the phrase "no-code programming" has attracted a lot of attention these days. Some examples of important LLMs for coding are, e.g., CodeBERT (Feng et al., 2020), GitHub Copilot (GitHub Copilot).
These topics constitute only the tip of the iceberg. The speed at which LLMs evolve is unprecedented. There are multiple extremely interesting new concepts, but, in my opinion, some directions are definitely overhyped. Nevertheless, Generative AI owes a lot to LLMs because they have changed the AI landscape and brought generative modeling to a completely new level.
References¶
(Almazrouei et al., 2023) Almazrouei, E., Alobeidli, H., Alshamsi, A., Cappelli, A., Cojocaru, R., Debbah, M., ... & Penedo, G. (2023). The falcon series of open language models. arXiv preprint arXiv:2311.16867.
(Bommasani et al., 2021) Bommasani, R., Hudson, D. A., Adeli, E., Altman, R., Arora, S., von Arx, S., ... & Liang, P. (2021). On the opportunities and risks of foundation models. arXiv preprint arXiv:2108.07258.
(Bondarenko et al., 2024) Bondarenko, Y., Nagel, M., & Blankevoort, T. (2024). Quantizable transformers: Removing outliers by helping attention heads do nothing. Advances in Neural Information Processing Systems, 36.
(Cho et al., 2014) Cho, K., Van Merriënboer, B., Gulcehre, C., Bahdanau, D., Bougares, F., Schwenk, H., & Bengio, Y. (2014). Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv preprint arXiv:1406.1078.
(Chomsky 1965) Chomsky, N. (1965). Aspects of the theory of syntax. Special technical report. Research laboratory of electronics. Massachusetts Institute of Technology.
(Chowdhery et al., 2023) Chowdhery, A., Narang, S., Devlin, J., Bosma, M., Mishra, G., Roberts, A., ... & Fiedel, N. (2023). Palm: Scaling language modeling with pathways. Journal of Machine Learning Research, 24(240), 1-113.
(Dao et al., 2022) Dao, T., Fu, D., Ermon, S., Rudra, A., & Ré, C. (2022). Flashattention: Fast and memory-efficient exact attention with io-awareness. Advances in Neural Information Processing Systems, 35, 16344-16359.
(Dauphin et al., 2017) Dauphin, Y. N., Fan, A., Auli, M., & Grangier, D. (2017). Language modeling with gated convolutional networks. In International conference on machine learning (pp. 933-941). PMLR.
(Devlin et al., 2018) Devlin, J., Chang, M. W., Lee, K., & Toutanova, K. (2018). BERT: Pre-training of deep bidirectional transformers for language understanding. arXiv preprint arXiv:1810.04805.
(Dong et al., 2019) Dong, L., Yang, N., Wang, W., Wei, F., Liu, X., Wang, Y., ... & Hon, H. W. (2019). Unified language model pre-training for natural language understanding and generation. Advances in neural information processing systems, 32.
(Dong et al., 2022) Dong, Q., Li, L., Dai, D., Zheng, C., Wu, Z., Chang, B., ... & Sui, Z. (2022). A survey on in-context learning. arXiv preprint arXiv:2301.00234.
(Fedus et al., 2022) Fedus, W., Dean, J., & Zoph, B. (2022). A review of sparse expert models in deep learning. arXiv preprint arXiv:2209.01667.
(Feng et al., 2020) Feng, Z., Guo, D., Tang, D., Duan, N., Feng, X., Gong, M., ... & Zhou, M. (2020). Codebert: A pre-trained model for programming and natural languages. arXiv preprint arXiv:2002.08155.
(Gage, 1994) Gage, P. (1994). A new algorithm for data compression. The C Users Journal, 12(2), 23-38.
(GitHub Copilot) “GitHub Copilot · Your AI pair programmer.” [Online]. Available: https://copilot.github.com/, Accessed: April 23, 2024
(Gu et al., 2021) Gu, A., Goel, K., and Re, C. (2021). Efficiently modeling long sequences with structured state spaces. In International Conference on Learning Representations
(Gu & Dao, 2023) Gu, A., & Dao, T. (2023). Mamba: Linear-time sequence modeling with selective state spaces. arXiv preprint arXiv:2312.00752.
(Hu et al., 2021) Hu, E.J., Shen, Y., Wallis, P., Allen-Zhu, Z., Li, Y., Wang, S., Wang, L. and Chen, W. (2021). Lora: Low-rank adaptation of large language models. arXiv preprint arXiv:2106.09685.
(Izdebski et al., 2023) Izdebski, A., Weglarz-Tomczak, E., Szczurek, E., & Tomczak, J. M. (2023). De Novo Drug Design with Joint Transformers. arXiv preprint arXiv:2310.02066.
(Jacobs et al., 1991) Jacobs, R. A., Jordan, M. I., Nowlan, S. J., & Hinton, G. E. (1991). Adaptive mixtures of local experts. Neural computation, 3(1), 79-87.
(Jiang et al., 2024) Jiang, Albert Q., Alexandre Sablayrolles, Antoine Roux, Arthur Mensch, Blanche Savary, Chris Bamford, Devendra Singh Chaplot et al. "Mixtral of experts." arXiv preprint arXiv:2401.04088 (2024).
(Jozefowicz et al., 2016) Jozefowicz, R., Vinyals, O., Schuster, M., Shazeer, N., & Wu, Y. (2016). Exploring the limits of language modeling. arXiv preprint arXiv:1602.02410.
(Kalchbrenner et al., 2014) Kalchbrenner, N., Grefenstette, E., & Blunsom, P. (2014). A convolutional neural network for modelling sentences. arXiv preprint arXiv:1404.2188.
(Kalchbrenner et al., 2016) Kalchbrenner, N., Espeholt, L., Simonyan, K., Oord, A. V. D., Graves, A., & Kavukcuoglu, K. (2016). Neural machine translation in linear time. arXiv preprint arXiv:1610.10099.
(Katharopoulos et al., 2020) Katharopoulos, A., Vyas, A., Pappas, N., & Fleuret, F. (2020). Transformers are rnns: Fast autoregressive transformers with linear attention. In International conference on machine learning (pp. 5156-5165). PMLR.
(Lieber et al., 2024) Lieber, O., Lenz, B., Bata, H., Cohen, G., Osin, J., Dalmedigos, I., ... & Shoham, Y. (2024). Jamba: A Hybrid Transformer-Mamba Language Model. arXiv preprint arXiv:2403.19887.
(Liu et al., 2019) Liu, Y., Ott, M., Goyal, N., Du, J., Joshi, M., Chen, D., ... & Stoyanov, V. (2019). Roberta: A robustly optimized bert pretraining approach. arXiv preprint arXiv:1907.11692.
(Luo et al., 2022) Luo, R., Sun, L., Xia, Y., Qin, T., Zhang, S., Poon, H., & Liu, T. Y. (2022). BioGPT: generative pre-trained transformer for biomedical text generation and mining. Briefings in bioinformatics, 23(6), bbac409.
(Ma et al., 2024) Ma, S., Wang, H., Ma, L., Wang, L., Wang, W., Huang, S., ... & Wei, F. (2024). The Era of 1-bit LLMs: All Large Language Models are in 1.58 Bits. arXiv preprint arXiv:2402.17764.
(Mikolov et al., 2010) Mikolov, T., Karafiát, M., Burget, L., Cernocký, J., & Khudanpur, S. (2010). Recurrent neural network based language model. In Interspeech (Vol. 2, No. 3, pp. 1045-1048).
(Mikolov et al., 2013) Mikolov, T., Sutskever, I., Chen, K., Corrado, G. S., & Dean, J. (2013). Distributed representations of words and phrases and their compositionality. Advances in neural information processing systems, 26.
(Ouyang et al., 2022) Ouyang, L., Wu, J., Jiang, X., Almeida, D., Wainwright, C., Mishkin, P., ... & Lowe, R. (2022). Training language models to follow instructions with human feedback. Advances in neural information processing systems, 35, 27730-27744.
(Pan et al., 2024) Pan, S., Luo, L., Wang, Y., Chen, C., Wang, J., & Wu, X. (2024). Unifying large language models and knowledge graphs: A roadmap. IEEE Transactions on Knowledge and Data Engineering.
(Peng et al., 2024) Peng, B., Goldstein, D., Anthony, Q., Albalak, A., Alcaide, E., Biderman, S., ... & Zhu, R. J. (2024). Eagle and Finch: RWKV with Matrix-Valued States and Dynamic Recurrence. arXiv preprint arXiv:2404.05892.
(Radford et al., 2018) Radford, A., Narasimhan, K., Salimans, T., & Sutskever, I. (2018). Improving language understanding by generative pre-training.
(Radford et al., 2019) Radford, A., Wu, J., Child, R., Luan, D., Amodei, D., & Sutskever, I. (2019). Language models are unsupervised multitask learners. OpenAI blog, 1(8), 9.
(Rafailov et al., 2024) Rafailov, R., Sharma, A., Mitchell, E., Manning, C. D., Ermon, S., & Finn, C. (2024). Direct preference optimization: Your language model is secretly a reward model. Advances in Neural Information Processing Systems, 36.
(Raffel et al., 2020) Raffel, C., Shazeer, N., Roberts, A., Lee, K., Narang, S., Matena, M., ... & Liu, P. J. (2020). Exploring the limits of transfer learning with a unified text-to-text transformer. Journal of machine learning research, 21(140), 1-67.
(Schulman et al., 2017) Schulman, J., Wolski, F., Dhariwal, P., Radford, A., & Klimov, O. (2017). Proximal policy optimization algorithms. arXiv preprint arXiv:1707.06347.
(Sun et al., 2023) Sun, Y., Dong, L., Huang, S., Ma, S., Xia, Y., Xue, J., Wang, J. and Wei, F. (2023). Retentive network: A successor to transformer for large language models. arXiv preprint arXiv:2307.08621.
(Touvron et al., 2023) Touvron, H., Martin, L., Stone, K., Albert, P., Almahairi, A., Babaei, Y., ... & Scialom, T. (2023). Llama 2: Open foundation and fine-tuned chat models. arXiv preprint arXiv:2307.09288.
(Vaswani et al., 2017) Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A.N., Kaiser, L. and Polosukhin, I. (2017). Attention is all you need. Advances in neural information processing systems, 30.
(Yang et al., 2019) Yang, Z., Dai, Z., Yang, Y., Carbonell, J., Salakhutdinov, R. R., & Le, Q. V. (2019). Xlnet: Generalized autoregressive pretraining for language understanding. Advances in neural information processing systems, 32.
(Zou et al., 2023) Zou, A., Wang, Z., Kolter, J. Z., & Fredrikson, M. (2023). Universal and transferable adversarial attacks on aligned language models. arXiv preprint arXiv:2307.15043.