Score-based Generative Models based on SDEs/ODEs

A reminder on diffusion-based models

Let us think about diffusion-based models again. We introduced them as hierarchical VAEs with very specific variational posteriors that were constructed as a linear transformation of previous latents and some added Gaussian noise. They could be also seen as a dynamical system with discretized time. To see that, let us say we transform a data point, $\mathbf{x}_{0}$, $\mathbf{x}_0 \sim p_{0}(\mathbf{x}) \equiv p_{data}(\mathbf{x})$ to noise, $\mathbf{x}_{1}$, sampled from a known distribution $\pi$, $\mathbf{x}_{1} \sim p_{1}(\mathbf{x}) \equiv \pi(\mathbf{x})$, the "time" is denoted by $t \in [0, 1]$, and there are $T$ steps between $\mathbf{x}_{0}$ and $\mathbf{x}_{1}$, namely, a step size is $\Delta = \frac{1}{T}$. Then we can represent the forward diffusion as follows:

\begin{equation} \mathbf{x}_{t+\Delta} = \sqrt{1 - \beta_t}\ \mathbf{x}_{t} + \sqrt{\beta_t}\ \epsilon_{t} , \end{equation}

where $\epsilon_{t} \sim \mathcal{N}(0, \mathbf{I})$. As you can notice, my curious reader, this is a dynamical system with discretized time. Please keep it in mind, we will come back to that later.

What is an interesting trait of diffusion-based models is that calculating $\mathbf{x}_{t}$ directly from data $\mathbf{x}_{0}$ is possible because of the linearity and Gaussianity, namely:

\begin{equation} \mathbf{x}_{t} = \sqrt{\alpha_t}\ \mathbf{x}_{0} + \sqrt{1 - \alpha_t}\ \epsilon_t, \end{equation}

where $\alpha_t = \prod_{\tau=1}^{t} (1 - \beta_{\tau})$. Further, we can calculate the datapoint back in the following manner:

\begin{equation} \mathbf{x}_{0} = \frac{1}{\sqrt{\alpha_t}}\ \mathbf{x}_{t} - \frac{\sqrt{1 - \alpha_t}}{\sqrt{\alpha_t}}\ \epsilon_t. \end{equation}

However, unlike in the forward diffusion in which we sample $\epsilon_t$, when we reverse $\mathbf{x}_{t}$ to $\mathbf{x}_{0}$, we do not have acces to the noise $\epsilon_t$. The standard situation is the following: We proceed with the forward diffusion until $\mathbf{x}_{t}$ and disregard all previous $\mathbf{x}$'s and $\epsilon$'s. However, not everything is lost! After all, we can introduce a neural network $\epsilon_{\theta}(\mathbf{x}_{t}, t)$ that aims for predicting the noise.

How to learn this neural network? In the seminal paper (Ho et al., 2020), the loss could be a sum of the following losses:

\begin{equation} \mathcal{L}_{t}(\theta) = \|\epsilon_{\theta}(\mathbf{x}_{t}, t) - \epsilon_{t}\|^{2}, \end{equation}

which was shown to be equivalent to the ELBO. But wait a second, do you see what I see, my curious reader? This loss is equivalent to another loss! Yes, it is score matching as presented in the post on score matching. There exists the following correspondence between the score model and the noise model (for Gaussian denoising distribution with the standard deviation $\sigma$):

\begin{equation} s_{\theta}(\mathbf{x}, t) = -\frac{\epsilon_{\theta}(\mathbf{x}_{t}, t)}{\sigma} . \end{equation}

Let us sum these considerations up:

• The forward diffusion defines a discrete-time dynamical system.
• The loss function for diffusion-based models is (almost) identical to the score matching loss.
• In fact, diffusion-based models correspond to score models.
• Diffusion-based models are very similar to score models trained with a schedule for $\sigma$ because both models are iterative and both models consider more noise at each step.

These similarities indicate that there may be an underlying framework that could generalize score models and diffusion-based models.

Stochastic/Ordinary Differential Equations as deep generative models

In the pursuit of a general framework Before we see an answer to this question about a general framework for score models and diffusion-based models, let us go back to the remark we did in the very beginning: "[diffusion-based models] could be also seen as a dynamical system with discretized time", because the forward diffusion is the following (we repeat it, but it never hurts to repeat something!):

\begin{equation} \mathbf{x}_{t+\Delta} = \sqrt{1 - \beta_t}\ \mathbf{x}_{t} + \sqrt{\beta_t}\ \epsilon_{t} . \end{equation}

We can be honest with each other, my curious reader, not everyone learned dynamical systems during their studies, or remember them. Before I worked on this post, my memory of ordinary differential equations (ODEs) and stochastic differential equations (SDEs) was very (very!) rusty. Therefore, let us delve into the world of differential equations very briefly! For more curious readers (yes, yes, I mean you!), I highly recommend the following book: (Särkkä & Solin, 2019). It is a great balance between basic and advanced topics.

Just a glipmse to the future: It turns out that SDEs and ODEs have a lot to offer for generative modeling. Hence, please stay with me and we will discover a new, beautiful world of a new class of generative models!

ODEs and numerical methods We start our discussion with ODEs. In general, we can define them as follows:

\begin{equation} \frac{\mathrm{d} \mathbf{x}_t}{\mathrm{d} t} = f(\mathbf{x}_{t}, t) , \end{equation}

with some initial conditions $\mathbf{x}_{0}$. Sometimes, $f(\mathbf{x}_{t}, t)$ is referred to as a vector field.

We can solve this ODE by running one of numerical methods that aim for discretizing time in a specific way. For instance, Euler's method carries it out in the following way (starting from $t=0$ and proceeding to $t=1$ with a step $\Delta$):

\begin{align} \mathbf{x}_{t+\Delta} - \mathbf{x}_{t} &= f(\mathbf{x}_{t}, t) \cdot \Delta \\ \mathbf{x}_{t+\Delta} &= \mathbf{x}_{t} + f(\mathbf{x}_{t}, t) \cdot \Delta . \end{align}

Sometimes, it is necessary to run from $t=1$ to $t=0$, then we can apply backward Euler's method:

\begin{equation} \mathbf{x}_{t} = \mathbf{x}_{t+\Delta} - f(\mathbf{x}_{t+\Delta}, t+\Delta) \cdot \Delta . \end{equation}

I know you, my brilliant reader, you see a connection, don't you? If we take $\mathbf{x}_0$ to be our data, and $\mathbf{x}_{1}$ to be noise, then if we knew $f(\mathbf{x}_{t}, t)$, we could run backward Euler's method to get a generative model! Please keep this thought in mind for now. But yes, you are right!

SDEs and Probability Flow ODEs Now, we will look into SDEs. In general, we can think of SDEs as ODEs whose trajectories are random and are distributed according to some probabilities at each $t$, $p_{t}(\mathbf{x})$. SDEs could be defined as follows:

\begin{equation} \mathrm{d} \mathbf{x}_{t} = f(\mathbf{x}_{t}, t) \mathrm{d} t + g(t) \mathrm{d} \mathbf{v}_{t} , \end{equation}

where $\mathbf{v}$ is a standard Wiener process, $f(\cdot, t)$ in this context is referred to as drift, and $g(\cdot)$ is a scalar function called diffusion. The drift component is deterministic (take a look at the formulation of ODEs above), but the diffusion element is stochastic due to the standard Wiener process (for more about Wiener processes, see (Särkkä & Solin, 2019); here, we do not need to know more than that they behave like Gaussians, e.g., the difference of its increments is normally distributed, $\mathbf{v}_{t+\Delta} - \mathbf{v}_{t} \sim \mathcal{N}(0,\Delta)$). A side note: The forms of drift and diffusion are assumed to be known. We will give an example later, for now just remember that they are given, my curious reader.

An important property of this SDE is the existence of a corresponding ordinary differential equation whose solutions follow the same distribution! If we start with a datapoint $\mathbf{x}_0$, we can get noise $\mathbf{x}_1 \sim p_{1}(\mathbf{x})$ by solving the following Probability Flow (PF) ODE (Song et al., 2020):

\begin{equation} \frac{\mathrm{d} \mathbf{x}_{t}}{\mathrm{d} t} = \left( f(\mathbf{x}_{t}, t) - \frac{1}{2}g^{2}(t) \nabla_{\mathbf{x}_{t}} \ln p_{t}(\mathbf{x}_{t}) \right) . \end{equation}

Let us take another look at that and see what we got:

• First of all, we do not have the Wiener process anymore. As a result, we deal with an ODE instead of an SDE.
• Second, the drift component and the diffusion components are still here, but the diffusion is multiplied by $-\frac{1}{2}$ and squared.
• Third, there is the score function! If you want to see a derivation, please check (Song et al., 2020), here we take it for granted as true. However, it looks reasonable. SDEs have solutions that are distributed according to $p_{t}(\mathbf{x})$, hence, it is not surprising that the score function pops up here. After all, the score function indicates how a trajectory should look like according to $p_{t}(\mathbf{x})$.

PF-ODEs as score-based generative models But wait a second! What do we have here? If we assume for a second that the score function is known, we can use this PF-ODE as a generative model by applying backward Euler's method starting from $\mathbf{x}_{1} \sim \pi(\mathbf{x})$:

\begin{equation} \mathbf{x}_{t} = \mathbf{x}_{t+\Delta} - \left( f(\mathbf{x}_{t+\Delta}, t+\Delta) - \frac{1}{2}g^{2}(t+\Delta) \nabla_{\mathbf{x}_{t+\Delta}} \ln p_{t}(\mathbf{x}_{t+\Delta}) \right) \cdot \Delta . \end{equation}

Perfect! Now, the problem is the score function but we know already how to deal with that, we can use denoising score matching (i.e., score matching with the noisy empirical distribution being a mixture of Gaussians centered at datapoints) for learning it. The difference to denoising score matching is that we need to take time $t$ into account:

\begin{equation} \mathcal{L}(\theta) = \int_{0}^{1} \mathcal{L}_t(\theta) \mathrm{d} t . \end{equation}

How to define $\mathcal{L}_t(\theta)$? The score matching idea tells us that we should consider $\lambda_t \| s_{\theta}(\mathbf{x}_t, t) - \nabla_{\mathbf{x}_t} \ln p_{t}(\mathbf{x}_t) \|^2$, but since we cannot calculate $p_{t}(\mathbf{x}_t)$, we should use something else. Instead, we can define a distribution $p_{0t}(\mathbf{x}_t|\mathbf{x}_0)$ that allows sampling noisy versions of our original datapoints $\mathbf{x}_0$'s. Putting it all together yields:

\begin{equation} \mathcal{L}_t(\theta) = \frac{1}{2} \mathbb{E}_{\mathbf{x}_0 \sim p_{data}(\mathbf{x})} \mathbb{E}_{\mathbf{x}_t \sim p_{0t}(\mathbf{x}_t|\mathbf{x}_0)} \left[ \lambda_t \| s_{\theta}(\mathbf{x}_t, t) - \nabla_{\mathbf{x}_t} \ln p_{0t}(\mathbf{x}_t|\mathbf{x}_0) \|^2 \right] . \end{equation}

Importantly, if we take $p_{0t}(\mathbf{x}_t|\mathbf{x}_0)$ to be Gaussian, then we could calculate the score function analytically. We will look into an example soon. Moreover, to calculate $\mathcal{L}_t(\theta)$ we can use a single sample (i.e., the Monte Carlo estimate).

After finding $s_{\theta}(\mathbf{x}_t, t)$, we can sample data by running backward Euler's method as follows:

\begin{equation} \mathbf{x}_{t} = \mathbf{x}_{t+\Delta} - \left( f(\mathbf{x}_{t+\Delta}, t+\Delta) - \frac{1}{2}g^{2}(t+\Delta) s_{\theta}(\mathbf{x}_{t+\Delta}, t + \Delta) \right) \cdot \Delta . \end{equation}

Please keep in mind that drift and diffusion are assumed to be known. Additionally, we stick to (backward) Euler's method, but you can pick another ODE solver, go ahead and be wild! But here, we want to be clear and as simple as possible.

In Figure 1, we present an example of using backward Euler's method for sampling. For some PF-ODE and a given score function, we can obtain samples from a multimodal distribution. As one may imagine, the ODE solver "goes" towards modes. In this simple example, we can notice that defining PF-ODEs is a powerful generative tool! Once the score function is properly approximated, we can sample from the original distribution in a straightforward manner.

Figure 1. An example of running backward Euler's method for a multimodal distribution. Here, we used $f(\mathbf{x}, t) = 0$, $g(t) = 9^t$, $T=100$, and the score function (not model!) was calculated using autograd. The green square denotes $\mathbf{x}_1 \sim \pi$, and the blue circle is a sample $\mathbf{x}_0$.

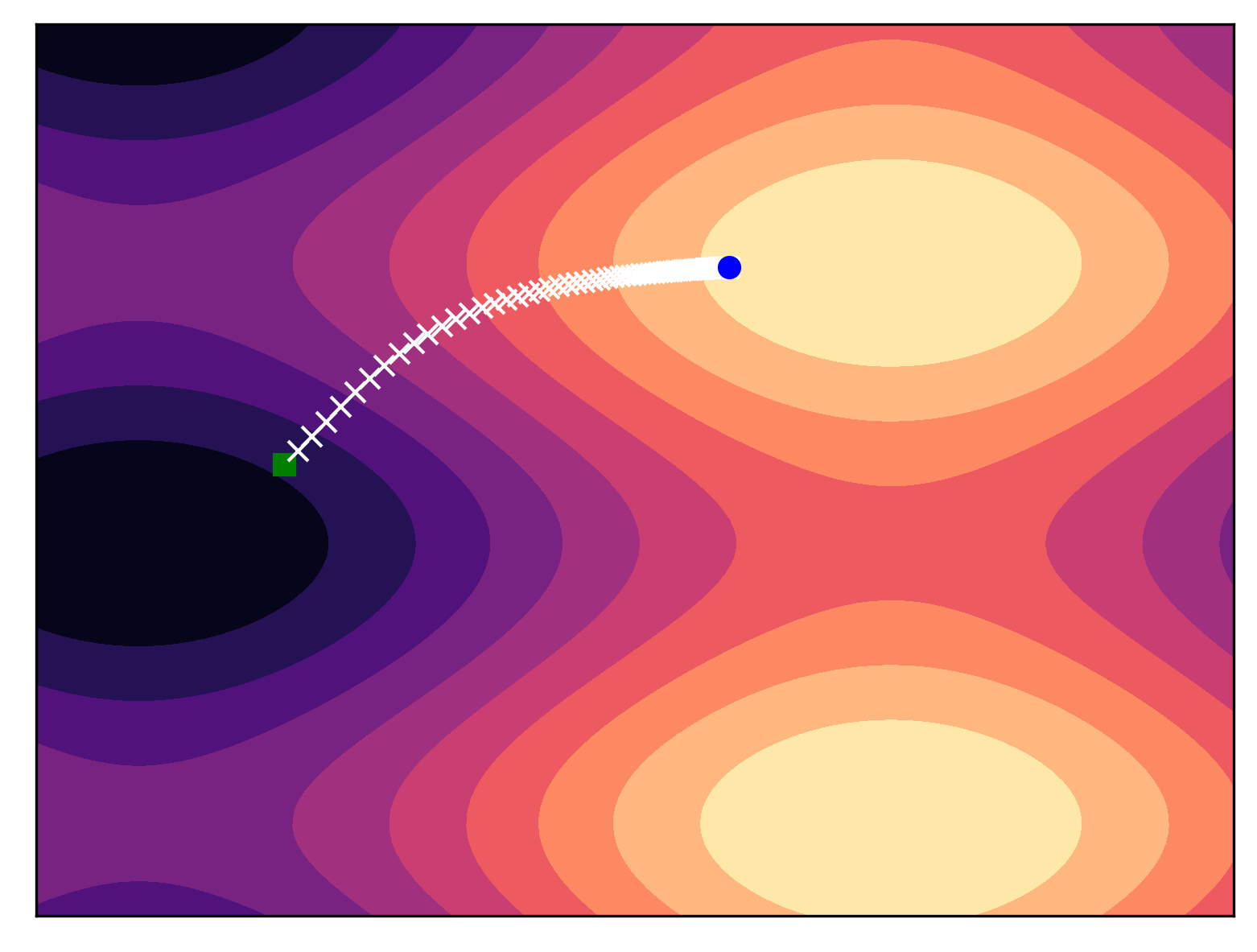
Alright, we have all the pieces to formualte our own score-based generative model (now it should be clear why this name, isn't it?).

An example of score-based generative models: Variance Exploding PF-ODE

Model formulation To define our own score-based generative model (SBGM), we need the following element:

• the drift $f(\mathbf{x}, t)$;
• the diffusion $g(t)$;
• and the form of $p_{0t}(\mathbf{x}_{t}|\mathbf{x}_0)$.

In (Song et al., 2020) and (Song et al., 2021) we can find three examples of SGBMs, namely, Variance Exploding (VE) SDE, Variance Preserving SDE, and sub-VP SDE. Here, we focus on the VE SDE.

In the VE SDE, we consider the following choices of the drift and the diffusion:

• $f(\mathbf{x}, t) = 0$,
• $g(t) = \sigma^{t}$, where $\sigma > 0$ is a hyperparameter; note that we take $\sigma$ to the power of time $t \in [0,1]$.

Then, according to our discussion above, plugin our choices for $f(\mathbf{x}, t)$ and $g(t)$ in the general form of the PF-ODE yields:

\begin{equation} \frac{\mathrm{d} \mathbf{x}_{t}}{\mathrm{d} t} = - \frac{1}{2} \sigma^{2t} \nabla_{\mathbf{x}_t} \ln p_{t}(\mathbf{x}_{t}) . \end{equation}

Now, to learn the score model, we need to define the conditional distribution for obtaining noisy version of $\mathbf{x}_0$. Fortunately, the theory of SDEs (e.g., see Chapter 5 of (Särkkä & Solin, 2019)) tells us how to calculate $p_{0t}(\mathbf{x}_{t}|\mathbf{x}_0)$! Specific formulas are presented in the Appendix of (Song et al., 2020). Here we provide the final solution:

\begin{equation} p_{0t}(\mathbf{x}_{t}|\mathbf{x}_0) = \mathcal{N}\left(\mathbf{x}_t | \mathbf{x}_0, \frac{1}{2 \ln \sigma}(\sigma^{2t} - 1) \mathbf{I}\right) , \end{equation}

thus, the variance function over time is the following:

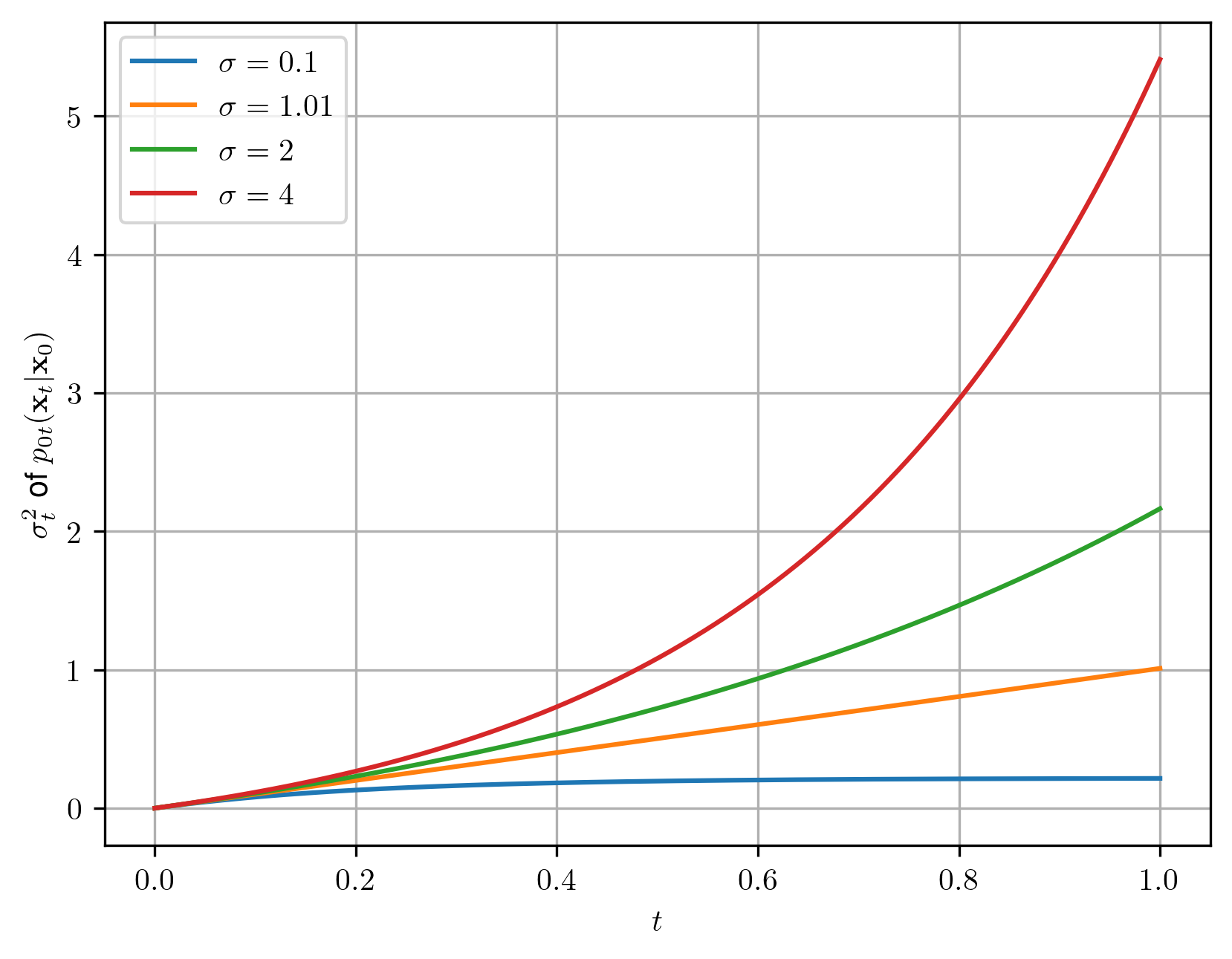
\begin{equation} \sigma_t^2 = \frac{1}{2 \ln \sigma}(\sigma^{2t} - 1). \end{equation}

Eventually, the final distribution, $p_{01}(\mathbf{x})$ gets approximately close to the following Gaussian (for sufficiently large $\sigma$):

\begin{align} p_{01}(\mathbf{x}) &= \int p_{0}(\mathbf{x}_0) * \mathcal{N} \left( \mathbf{x} | \mathbf{x}_{0}, \frac{1}{2 \ln \sigma}(\sigma^{2} - 1)\mathbf{I} \right) \\ &\approx \mathcal{N}\left( \mathbf{x} | 0, \frac{1}{2 \ln \sigma}(\sigma^{2} - 1)\mathbf{I} \right) . \end{align}

We will use $p_{01}(\mathbf{x})$ to sample noise $\mathbf{x}_1$ and then for reverting it to data $\mathbf{x}_0$.

To better understand how various values of $\sigma$ influence $\sigma_{t}$, we can have a look at curves in Figure 2. For obvious reasons, we cannot pick $\sigma = 1$ (why, you ask? well, $ln(1) = 0$, so we get into an issue of dividing by 0), but for $\sigma=1.01$ we get $p_1(\mathbf{x})$ close to the standard Gaussian.

Figure 2. The dependency of the standard deviation of $p_{0t}(\mathbf{x}_{t}|\mathbf{x}_0)$ on $t$ for different choices of $\sigma$.

The choice of $\lambda_t$ The last remark, before we move to the training procedure, is about the choice of $\lambda_{t}$ in the definition of $\mathcal{L}_t(\theta)$. So far, I simply omitted that but I had a good reason. (Ho et al., 2020) simply set $\lambda_t \equiv 1$. Done! Really though? Well, as you can imagine, but smart reader, that is not so easy. (Song et al., 2021) showed that it is actually beneficial to set $\lambda_t = \sigma_t^2$ in the case of VE PF-ODE. Then, we can even use the sum over $\mathcal{L}_t(\theta)$ as a proxy to the log-likelihood function. We will take advantage of that for early-stopping in our training procedure.

Training of SBDMs We will present training procedure basing on the chosen example of the VE SDM. As we outlined earlier in the case of the score matching method, the procedure is relatively easy and straightforward. It consists of the following steps:

1. Pick a datapoint $\mathbf{x}_0$.
2. Sample $\mathbf{x}_1 \sim \pi(\mathbf{x}) = \mathcal{N}\left( \mathbf{x} | 0, \mathbf{I} \right)$.
3. Sample $t \sim \mathrm{Uniform}(0,1)$.
4. Calculate $\mathbf{x}_t = \mathbf{x}_0 + \sqrt{\frac{1}{2 \ln \sigma}(\sigma^{2t} - 1)} \cdot \mathbf{x}_{1}$. This is a sample from $p_{0t}(\mathbf{x}_{t}|\mathbf{x}_{0})$.
5. Evaluate the score model at $\mathbf{x}_t$ and $t$, $s_{\theta}(\mathbf{x}_t, t)$.
6. Caclulate the score matching loss for a single sample, $\mathcal{L}_{t}(\theta) = \sigma_{t}^2 \| \mathbf{x}_1 - \sigma_t s_{\theta}(\mathbf{x}_t, t) \|^2$.
7. Update $\theta$ using a gradient-based method with $\nabla_{\theta} \mathcal{L}_{t}(\theta)$.

We repeat these 7 steps for available training data until some stop criterion is met. Obviously, in practice, we use mini-batches instead of single datapoints.

In this training procedure we use $-\sigma_t s_{\theta}(\mathbf{x}_t, t)$ on purpose because $-\sigma_t s_{\theta}(\mathbf{x}_t, t) = \epsilon_{\theta}(\mathbf{x}_t, t)$ and then the criterion $\sigma_{t}^2 \| \mathbf{x}_1 - \epsilon_{\theta}(\mathbf{x}_t, t) \|^2$ corresponds to diffusion-based models (Kingma et al., 2021; Kingma & Gao, 2023). Now you see why we pushed for seeing diffusion-based models as dynamical systems!

Sampling After training the score model, we can finally generate! For that, we need to run backward Euler's method (or other ODE solvers, please remember that) that takes the following form for the VE PF-ODE:

\begin{align} \mathbf{x}_{t} &= \mathbf{x}_{t+\Delta} + \left( \frac{1}{2}\sigma^{2(t+\Delta)} \left\{ - \frac{1}{\sigma^{t+\Delta}} s_{\theta}(\mathbf{x}_{t+\Delta}, t + \Delta) \right\} \right) \cdot \Delta \\ &= \mathbf{x}_{t+\Delta} - \left( \frac{1}{2}\sigma^{t+\Delta} s_{\theta}(\mathbf{x}_{t+\Delta}, t + \Delta) \right) \cdot \Delta \end{align}

starting from $\mathbf{x}_1 \sim p_{01}(\mathbf{x}) = \mathcal{N}\left( \mathbf{x} | 0, \frac{1}{2 \ln \sigma}(\sigma^{2} - 1)\mathbf{I} \right)$. Note that in the first line we have the plus sign because the diffusion for the VE PF-ODE is $-\frac{1}{2} \sigma^{2t}$, therefore, the minus sign in backward Euler's method turns to plus. Maybe this is very obvious for you, my reader, but I alwasy mess around with pluses and minuses, so I prefer to be very precise here.

Finally some code!

We have everything ready for implementing our VE SDGM! Similarly to score matching, we transform data to be in $[-1, 1]$. As you will notice, this code shares many similarities to the code of score matching. But this is to be expected since they are conceptually very similar.

The full code (with auxiliary functions) that you can play with is available here: link.

class SBGM(nn.Module):
    def __init__(self, snet, sigma, D, T):
        super(SBGM, self).__init__()

        print("SBGM by JT.")
        
        # sigma parameter
        self.sigma = torch.Tensor([sigma])
        
        # define the base distribution (multivariate Gaussian with the diagonal covariance)
        var = (1./(2.* torch.log(self.sigma))) * (self.sigma**2 - 1.)
        self.base = torch.distributions.multivariate_normal.MultivariateNormal(torch.zeros(D), var * torch.eye(D))
        
        # score model
        self.snet = snet
        
        # time embedding (a single linear layer)
        self.time_embedding = nn.Sequential(nn.Linear(1, D), nn.Tanh())
        
        # other hyperparams
        self.D = D
        
        self.T = T
                
        self.EPS = 1.e-5
        
    def sigma_fun(self, t):
        # the sigma function (dependent on t), it is the std of the distribution
        return torch.sqrt((1./(2. * torch.log(self.sigma))) * (self.sigma**(2.*t) - 1.))

    def log_p_base(self, x):
        # the log-probability of the base distribition, p_1(x)
        log_p = self.base.log_prob(x)
        return log_p
    
    def sample_base(self, x_0):
        # sampling from the base distribution
        return self.base.rsample(sample_shape=torch.Size([x_0.shape[0]]))
        
    def sample_p_t(self, x_0, x_1, t):
        # sampling from p_0t(x_t|x_0)
        # x_0 ~ data, x_1 ~ noise
        x = x_0 + self.sigma_fun(t) * x_1
        
        return x
    
    def lambda_t(self, t):
        # the loss weighting
        return self.sigma_fun(t)**2
    
    def diffusion_coeff(self, t):
        # the diffusion coefficient in the SDE
        return self.sigma**t
    
    def forward(self, x_0, reduction='mean'):
        # =====
        # x_1 ~ the base distribiution
        x_1 = torch.randn_like(x_0)
        # t ~ Uniform(0, 1)
        t = torch.rand(size=(x_0.shape[0], 1))  * (1. - self.EPS) + self.EPS 
        
        # =====
        # sample from p_0t(x|x_0)
        x_t = self.sample_p_t(x_0, x_1, t)

        # =====
        # invert noise
        # NOTE: here we use the correspondence eps_theta(x,t) = -sigma*t score_theta(x,t)
        t_embd = self.time_embedding(t)
        x_pred = -self.sigma_fun(t) * self.snet(x_t + t_embd)

        # =====LOSS: Score Matching
        # NOTE: since x_pred is the predicted noise, and x_1 is noise, this corresponds to Noise Matching 
        #       (i.e., the loss used in diffusion-based models by Ho et al.)
        SM_loss = 0.5 * self.lambda_t(t) * torch.pow(x_pred + x_1, 2).mean(-1)
        
        if reduction == 'sum':
            loss = SM_loss.sum()
        else:
            loss = SM_loss.mean()

        return loss

    def sample(self, batch_size=64):
        # 1) sample x_0 ~ Normal(0,1/(2log sigma) * (sigma**2 - 1))
        x_t = self.sample_base(torch.empty(batch_size, self.D))
        
        # Apply Euler's method
        # NOTE: x_0 - data, x_1 - noise
        #       Therefore, we must use BACKWARD Euler's method! This results in the minus sign! 
        ts = torch.linspace(1., self.EPS, self.T)
        delta_t = ts[0] - ts[1]
        
        for t in ts[1:]:
            tt = torch.Tensor([t])
            u = 0.5 * self.diffusion_coeff(tt) * self.snet(x_t + self.time_embedding(tt))
            x_t = x_t - delta_t * u
        
        x_t = torch.tanh(x_t)
        return x_t
    
    def log_prob_proxy(self, x_0, reduction="mean"):
        # Calculate the proxy of the log-likelihood (see (Song et al., 2021))
        # NOTE: Here, we use a single sample per time step (this is done only for simplicity and speed);
        # To get a better estimate, we should sample more noise
        ts = torch.linspace(self.EPS, 1., self.T)

        for t in ts:
            # Sample noise
            x_1 = torch.randn_like(x_0)
            # Sample from p_0t(x_t|x_0)
            x_t = self.sample_p_t(x_0, x_1, t)
            # Predict noise
            t_embd = self.time_embedding(torch.Tensor([t]))
            x_pred = -self.snet(x_t + t_embd) * self.sigma_fun(t)
            # loss (proxy)          
            if t == self.EPS:
                proxy = 0.5 * self.lambda_t(t) * torch.pow(x_pred + x_1, 2).mean(-1)
            else:
                proxy = proxy + 0.5 * self.lambda_t(t) * torch.pow(x_pred + x_1, 2).mean(-1)
            
        if reduction == "mean":
            return proxy.mean()
        elif reduction == "sum":
            return proxy.sum()

After running the code with an MLP-based scoring model, and the following values of the hyperparameters $\sigma = 1.01$ and $T=20$, we can expect results like in Figure 2.

A

B

C

Figure 2. A. A sample of real images. B. A sample of generated images. C. An example of the score matching loss calculated on the validation set.

I rarely comment on the results, especially that the dataset I use is oversimplistic (but on purpose, so that you can run the code quickly!). However, I want to point out two things:

• The VE-SBGM is not a very easy to model to work with because it is pretty noisy. Inspecting the generated images gives a good feeling of potential issues. We run the ODE solver for $20$ steps. However, SBGMs require typically hundreds or ever thousends of steps.
• Take a look at the validation value of the proxy. It is a known fact that the convergence speed of SBGMs is rather slow.

There is a fantastic world of score-based generative models out there!

Other SBGMs There are other classes of SBGMs beside Variance Exploding, namely (Song et al., 2020):

• Variance Preserving (VP): the drift is $f(\mathbf{x}, t) = - \frac{1}{2} \beta_t \mathbf{x}$, the diffusion is $g(t) = \sqrt{\beta_t}$, and the loss weighting is $\lambda_t = 1 - \exp\{- \int_{0}^{t} \beta_s \mathrm{d}s\}$, where $\beta_t$ is some function of time $t$.
• sub-VP: the drift is $f(\mathbf{x}, t) = - \frac{1}{2} \beta_t \mathbf{x}$, the diffusion is $g(t) = \sqrt{\beta_t \left( 1 - \exp\{- 2\int_{0}^{t} \beta_s \mathrm{d}s\} \right)}$, and the loss weighting is $\lambda_t = \left( 1 - \exp\{- \int_{0}^{t} \beta_s \mathrm{d}s\} \right)^2$, where $\beta_t$ is some function of time $t$.

There exist various versions of these models, especially there are different ways of defining $\lambda_t$ and other functions dependent on $t$ like $\sigma_t$ in VE and $\beta_t$ in VP. See (Kingma & Gao, 2023) for an overview.

Better solvers As briefly mentioned earlier, one drawback of SBGMs is a large number of steps during sampling (i.e., the number of steps of an ODE solver). (Lu et al., 2022) presented a specialized ODE solvers that could achieve great performance within $T=10$ that was further improved to $T=5$ in (Zhou et al., 2023)! In general, a better-suited solver could be used to obtain better results, e.g., by using Heun's method (Karras et al., 2022).

Other improvements There are many ideas within the domain of score-based models! Here, I will name only a few:

• Using SBGMs in the latent space (Vahdat et al., 2021).
• In fact, it is possible to calculate the log-likelihood function for SBGMs in a similar manner to neural ODE (Chen et al., 2018). (Song et al., 2021) showed that the log-likehood function could be upper-bounded by some modification of the score matching loss.
• Using various tricks to improve the log-likelihood estimation like dequantization and importance-weighting (Zheng et al., 2023).
• In (Song et al., 2023) a new class of models was proposed dubbed consistency models. The idea is to learn a model that could match noise to data in a single step.
• An extension of SBGMs to Remaniann manifolds was proposed in (De Bortoli et al., 2022).

There is a lot of work done! There are many, many papers on SBGMs being published as we speak. Check out this webpage for up-to-date overview of SBGMs: [link].

References

(Chen et al., 2018) Chen, R.T., Rubanova, Y., Bettencourt, J. and Duvenaud, D.K., 2018. Neural ordinary differential equations. Advances in neural information processing systems, 31.

(De Bortoli et al., 2022) De Bortoli, V., Mathieu, E., Hutchinson, M., Thornton, J., Teh, Y.W. and Doucet, A., 2022. Riemannian score-based generative modelling. Advances in Neural Information Processing Systems, 35, pp.2406-2422.

(Ho et al., 2020) Ho, J., Jain, A. and Abbeel, P., 2020. Denoising diffusion probabilistic models. Advances in neural information processing systems, 33, pp.6840-6851.

(Karras et al., 2022) Karras, T., Aittala, M., Aila, T. and Laine, S., 2022. Elucidating the design space of diffusion-based generative models. Advances in Neural Information Processing Systems, 35, pp.26565-26577.

(Kingma & Gao, 2023) Kingma, D.P. and Gao, R., 2023, November. Understanding diffusion objectives as the ELBO with simple data augmentation. In Thirty-seventh Conference on Neural Information Processing Systems.

(Lu et al., 2022) Lu, C., Zhou, Y., Bao, F., Chen, J., Li, C. and Zhu, J., 2022. Dpm-solver: A fast ode solver for diffusion probabilistic model sampling in around 10 steps. Advances in Neural Information Processing Systems, 35, pp.5775-5787.

(Särkkä & Solin, 2019) Särkkä, S. and Solin, A., 2019. Applied stochastic differential equations (Vol. 10). Cambridge University Press.

(Song et al., 2020) Song, Y., Sohl-Dickstein, J., Kingma, D. P., Kumar, A., Ermon, S., & Poole, B. (2020). Score-based generative modeling through stochastic differential equations. arXiv preprint arXiv:2011.13456.

(Song et al., 2021) Song, Y., Durkan, C., Murray, I. and Ermon, S., 2021. Maximum likelihood training of score-based diffusion models. Advances in Neural Information Processing Systems, 34, pp.1415-1428.

(Song et al., 2023) Song, Y., Dhariwal, P., Chen, M. and Sutskever, I., 2023. Consistency models. arXiv preprint arXiv:2303.01469.

(Vahdat et al., 2021) Vahdat, A., Kreis, K. and Kautz, J., 2021. Score-based generative modeling in latent space. Advances in Neural Information Processing Systems, 34, pp.11287-11302.

(Zhou et al., 2023) Zhou, Z., Chen, D., Wang, C. and Chen, C., 2023. Fast ODE-based Sampling for Diffusion Models in Around 5 Steps. arXiv preprint arXiv:2312.00094.